Informationen zum Netz
In der Regel wird das Netz nicht in der Grafik angezeigt. In den folgenden Grafiken wird veranschaulicht, wie das Netz aussehen könnte.
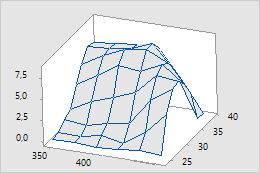
3D-Drahtgitterdiagramm und 3D-Wirkungsflächendiagramm
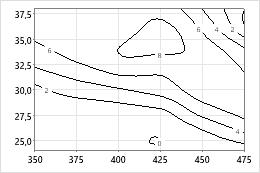
Konturdiagramm
Tipp
Wählen Sie aus, um ein reguläres Gitter aus x-y-Positionen der Stichprobe oder Faktorkombinationen zu erstellen. Sie können anschließend Ihre eigenen z-Spalten hinzufügen oder aus einer Liste von Funktionen auswählen.
Wie stellt Minitab die Daten der Antwortvariablen auf einem Netz dar?
Minitab trägt die Werte der Antwortvariablen (z) an den x-y-Schnittpunkten eines gleichmäßigen Gitters auf. Wenn Ihre x- und y-Werte gleichmäßige Abstände aufweisen, trägt Minitab die z-Werte an den x-y-Schnittpunkten auf. Wenn Ihre x- und y-Werte keine regelmäßigen Abstände aufweisen, interpoliert (schätzt) Minitab die z-Werte an den Schnittpunkten eines regulären 15x15-Netzes mit denselben x- und y-Spannweiten wie in Ihren Daten.
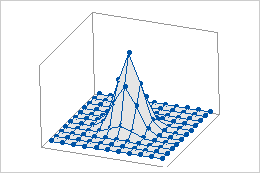
Daten auf einem regulären Netz
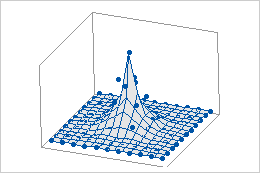
Daten auf einem irregulären Netz
Die Symbole in diesen Grafiken stellen die tatsächlichen (nicht die interpolierten) Datenpunkte dar. Bei einem regulären Netz werden die z-Werte an den x-y-Schnittpunkten aufgetragen. Wenn die x- und y-Werte kein reguläres Netz bilden, werden die z-Werte nicht an den Schnittpunkten aufgetragen.
Hinweis
Die Symbole und Projektionslinien stellen immer die tatsächlichen (nicht die interpolierten) Datenpunkte dar.
Ändern der Interpolationsmethode für ein irreguläres Netz
Wenn Ihre x- und y-Werte keine regelmäßigen Abstände aufweisen, interpoliert (schätzt) Minitab die z-Werte an den Schnittpunkten eines regulären 15x15-Netzes mit denselben x- und y-Spannweiten wie in Ihren Daten. Sie können die von Minitab verwendete Interpolationsmethode ändern. Wenn Sie sich nicht sicher sind, welche Methode Sie verwenden sollten, empfiehlt es sich möglicherweise, beide Methoden auszuprobieren und sich für die besser für Ihre Daten geeignete zu entscheiden.
Hinweis
Wenn Ihre x- und y-Werte ein Gitter mit gleichmäßigen Abständen bilden, wirkt sich die Interpolationsmethode nicht auf Ihr Diagramm aus.
- Klicken Sie im Dialogfeld für die Grafik, die Sie erstellen, auf Wirkungsflächenoptionen oder auf Konturoptionen.
- Wählen Sie auf der Registerkarte Methode eine Interpolationsmethode aus.
- Distanzmethode
- Die Distanzmethode (Standardeinstellung) eignet sich gut für viele Situationen. Sie ist in dem Sinne konservativ, dass sie für z immer Schätzwerte berechnet, die innerhalb der Spannweite Ihrer Daten liegen.
- Polynomialmethode nach Akima
- Diese Methode eignet sich in einigen Fällen gut, weist jedoch in anderen Fällen unerwünschte Effekte auf. Da bei dieser Methode ein Polynom fünfter Ordnung verwendet wird, resultieren möglicherweise zu große oder kleine z-Werte an x-y-Positionen, die jenseits der von Ihnen erfassten Stichprobenwerte liegen.
Unter diesen Bedingungen die Distanzmethode verwenden Unter diesen Bedingungen die Polynomialmethode nach Akima verwenden Ihre Wirkungsfläche weist isolierte Extremwerte oder sprunghafte Übergänge auf. Ihre Wirkungsfläche ändert sich sanft über die x- und y-Spannweite Ihrer Daten. Die Stichprobe ist nicht gründlich genug, um sanfte Wirkungsflächenübergänge zu erfassen. Die Stichprobe ist gründlich genug, um sanfte Wirkungsflächenübergänge zu erfassen. Der Stichprobenfehler ist groß. Der Stichprobenfehler ist im Verhältnis zur Wirkungsfläche klein. - Klicken Sie auf OK.
- (Optional) Veranschaulichen Sie die Positionen der x- and y-Daten durch Hinzufügen von Symbolen im Diagramm.
- Doppelklicken Sie auf die Grafik.
- Klicken Sie mit der rechten Maustaste auf die Grafik, und wählen Sie aus.
- Wählen Sie Symbole aus, und klicken Sie dann auf OK.
Tipp
Aus den folgenden Gründen kann es nützlich sein, die Positionen der x- und y-Daten zu veranschaulichen:
- Wenn Sie die Polynomialmethode nach Akima verwenden, kann das Anzeigen von Symbolen hilfreich sein, um nach starken Veränderungen außerhalb der x- und y-Daten zu suchen, die nicht unterstützt würden, wenn Sie Stichproben in diesem Bereich gezogen hätten.
- Wenn Sie die Distanzmethode verwenden, kann das Anzeigen von Symbolen hilfreich bei der Auswahl der Ordnung der Distanz sein. In diesem Fall sehen Sie, wie die Prognosen über die x- und y-Daten hinausreichen.
Was ist die Netzauflösung?
Die Anzahl der x- und y-Werte in einem Netz bestimmt dessen Auflösung. Ein höher aufgelöstes Netz (eines mit mehr x- und y-Werten) ergibt eine feinere Interpolation der Wirkungsfläche oder Konturen. Die folgenden Drahtgitter- und Konturdiagramme zeigen dieselben Daten, verwenden jedoch unterschiedliche Netzauflösungen. (Die Gitterlinien in den Konturdiagrammen zeigen die ungefähre Netzposition an.)
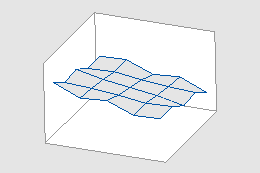
5x5-Netz bei Drahtgitterdiagrammen

15x15-Netz bei Drahtgitterdiagrammen
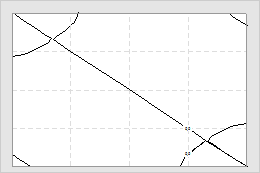
5x5-Netz bei Konturdiagrammen

15x15-Netz bei Konturdiagrammen
Korrigieren der Netzauflösung
Wenn die x-y-Daten kein reguläres Gitter bilden, kann die Netzauflösung bedeutsame Auswirkungen auf ein Kontur- oder Wirkungsflächendiagramm haben. Wenn die Stichprobe derart beschaffen ist, dass die x-y-Punkte nahe bei einem regulären Gitter liegen, verbessert es möglicherweise die Anpassung, wenn Sie ein Netz festlegen, das Ihren Daten ähnelt.
Angenommen, Sie möchten den Effekt von Temperatur und Druck auf die Garzeit untersuchen. Es liegen vier Temperatureinstellungen (325, 350, 375, 400) und drei Druckeinstellungen (5, 10, 15) vor. Beim Durchführen des Experiments wich die Temperatur in einigen Durchläufen jedoch leicht von der gewünschten Einstellung ab, und daher bilden die Daten ein leicht irreguläres Gitter. Da die Temperaturwerte jedoch fast regulär sind, könnte ein 4x3-Netz (Temperatur x Druck) vorteilhaft für Ihre Kontur- und 3D-Wirkungsflächendiagramme sein.
Hinweis
Ein Netz mit mehr und kleineren Intervallen als tatsächlich zwischen Datenpunkten vorhanden lässt die Grafik stärker aufgelöst erscheinen, aber bei den dadurch gewonnenen Details handelt es sich wahrscheinlich nur um Hintergrundrauschen.
- Doppelklicken Sie auf die Wirkungsfläche.
- Doppelklicken Sie auf das 3D-Wirkungsflächendiagramm oder das 3D-Konturdiagramm.
- Führen Sie auf der Registerkarte Methode folgende Aktionen aus:
- Wählen Sie unter Netz zum Interpolieren der Wirkungsfläche die Option Benutzerspezifisch aus.
- Geben Sie für die gewünschte Netzauflösung X-Netz-Zahl und Y-Netz-Zahl ein.
