Ein Ernährungsberatungsunternehmen hat ein Bildungsprogramm entwickelt, um die Kalziumaufnahme bei Kindern von 9 bis 13 Jahren zu fördern. Um die Effektivität des Programms zu messen, führt ein Analytiker ein Experiment durch, bei dem 200 Kinder nach dem Zufallsprinzip entweder der Kontrollgruppe (kein Bildungsprogramm) oder der Experimentalgruppe zugewiesen werden. Die durchschnittliche tägliche Kalziumaufnahme mit der Nahrung wird anhand von Ernährungsprotokollen über 3 Tage berechnet.
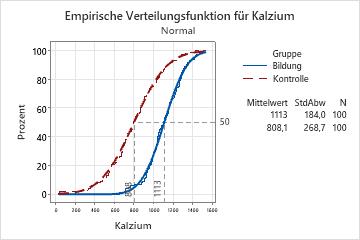
Der Analytiker erstellt ein Diagramm der empirischen Verteilungsfunktion, um die Verteilung der Kalziumaufnahme für jede Gruppe zu untersuchen. Insbesondere möchte er die Werte für die Kalziumaufnahme jeder Gruppe ermitteln, die unterhalb des 50. Perzentils liegen.
- Öffnen Sie die Beispieldaten Kalziumaufnahme.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Grafikvariablen die Spalte Kalzium ein.
- Geben Sie im Feld Kategoriale Gruppierungsvariablen (0-3) die Spalte Gruppe ein.
- Klicken Sie auf OK.
- Klicken Sie mit der rechten Maustaste auf die Grafik, und wählen Sie aus.
- Geben Sie im Feld Perzentillinien bei Y-Werten anzeigen den Wert 50 ein.
- Klicken Sie auf OK.
- Zeigen Sie mit dem Mauszeiger auf Punkte auf der Verbindungslinie, um die tatsächlichen Datenwerte (x) und Perzentile (y) abzurufen.
Interpretieren der Ergebnisse
Die Datenpunkte für beide Gruppen liegen dicht an den angepassten Linien der Normalverteilung. Die Perzentillinien zeigen, dass etwa 50 % der Kinder in der Kontrollgruppe Kalziumaufnahmewerte von mindestens 808 aufweisen, während sich die Kalziumaufnahme von 50 % der Kinder in der Experimentalgruppe auf mindestens 1113 beläuft.
Durch Verschieben des Mauszeigers auf den Verbindungslinien stellt der Analytiker fest, dass eine Kalziumaufnahme von 1000 annähernd dem 76. Perzentil der Kontrollgruppe und ungefähr dem 25. Perzentil der Experimentalgruppe entspricht. Daher ist für etwa 76 % der Kinder in der Kontrollgruppe und 25 % der Kinder in der Experimentalgruppe eine Kalziumaufnahme von weniger als 1000 zu beobachten.
Hinweis
Weitere Informationen zu Optionen für angepasste Verteilungslinien finden Sie unter Angepasste Verteilungslinien.
