In der Standardeinstellung befindet sich der untere Rand der Box am 1. Quartil (Q1), und der obere Rand befindet sich am 3. Quartil (Q3). Die Whisker sind die Linien, die sich vom unteren und oberen Rand der Box zu den angrenzenden Werten erstrecken. Die angrenzenden Werte sind die niedrigste und die höchste Beobachtung, die sich noch im Bereich befinden, der durch die folgenden Grenzen definiert wird:
- Untergrenze = Q1 – 1,5 (Q3 – Q1)
- Obergrenze = Q3 + 1,5 (Q3 – Q1)
Der obere angrenzende Wert kann jedoch kleiner als Q3 sein, wodurch der Whisker zwangsläufig von Q3 in die Box gezogen wird. Der untere angrenzende Wert kann ebenfalls größer als Q1 sein, wodurch der Whisker gezwungenermaßen von Q1 in die Box gezogen wird.
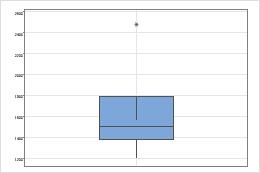
Beispiel für ein Boxplot mit einem „eingewachsenen“ Whisker
Dieses Boxplot zeigt die folgenden Daten: 1200 1443 1490 1528 1563 2479.
Für dieses Boxplot:
- Q1 = 1382
- Q3 = 1792
- Untergrenze = 1382 – 1,5*(1792 – 1382) = 767
- Obergrenze = 1792 + 1,5*(1792 – 1382) = 2407
Die kleinste Beobachtung innerhalb dieses Bereichs ist 1200 und die größte ist 1563. Der untere Whisker verbindet Q1=1382 mit 1200, was außerhalb der Box liegt. Der obere Whisker verbindet Q3=1792 mit 1536, wodurch er sich in die Box erstreckt.
Hinweis
Wenn Sie Hinges anstelle von Quartilen für die Endpunkte der Box verwenden, können Whisker niemals „einwachsen“.
