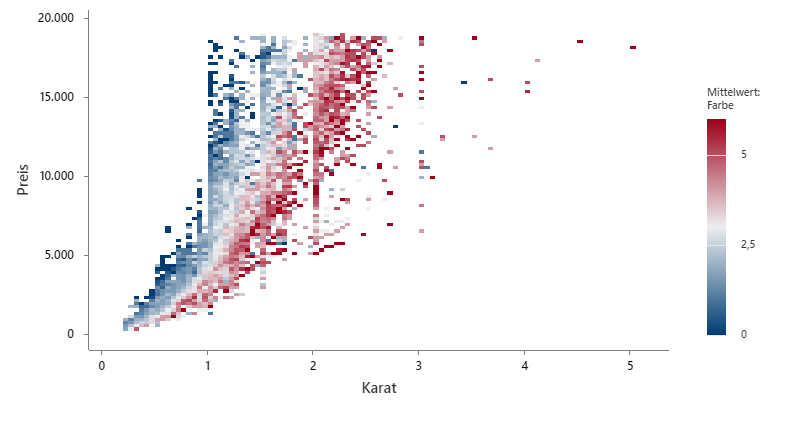
Ein Forscherteam für einen großen Schmuckhändler möchte die Beziehung zwischen Karatzahl, Farbe und Preis verschiedener Diamanten untersuchen. Ein Streudiagramm lässt sich wegen des großen Datensatzes nur schwer interpretieren. Daher entscheidet sich das Team für ein Streudiagramm mit Einteilungen, damit die Grafik leichter interpretiert werden kann.
Hinweis
In der Regel wird die Farbe eines Diamanten mit einem Buchstaben dargestellt. Da alle Variablen numerisch sein müssen, kodieren die Forscher die Farbe des Diamanten auf einer numerischen Skala von 0–6. Die Forscher weisen farblosen Diamanten eine höhere Zahl zu, während hellgelbe Diamanten eine niedrigere Zahl erhalten.
- Öffnen Sie die Beispieldaten Diamanten.MWX.
- Wählen Sie aus.
- Geben Sie im Feld Y-Variable die Spalte Preis ein.
- Geben Sie im Feld X-Variable die Spalte Karat ein.
- Wählen Sie Mittelwert der Variablen aus, und geben Sie Farbe ein.
- Klicken Sie auf OK.
Interpretieren der Ergebnisse
Minitab gruppiert die Daten in rechteckigen Einteilungen. Minitab verwendet für die Einteilungen die Farben Dunkelblau bis Dunkelrot in Abhängigkeit von der Farbe des Diamanten. Ein dunkleres Rot entspricht höheren Werten der Farbvariablen. Ein dunkleres Blau entspricht niedrigeren Werten der Farbvariablen. Das Forscherteam möchte ermitteln, wie sich Karatzahl und Farbe auf den Preis auswirken. Der Preis des Diamanten steigt mit zunehmender Karatzahl. Die Streuung bei den Preisen für Diamanten mit derselben Karatzahl ist jedoch immer noch hoch. Die Farbe des Diamanten erklärt einen Teil dieser Streuung. Bei Diamanten mit derselben Karatzahl entspricht eine höhere Farbnummer einem höheren Preis.