Um diese Funktion zu verwenden, wählen Sie aus.
Diese Funktion berechnet den Exponenten, mit dem 10 potenziert werden muss, um eine angegebene Zahl zu erreichen. Zum Beispiel ist 102 = 100, daher ist der Logarithmus von 100 zur Basis 10 gleich 2. Der Logarithmus zur Basis 10 ist nur für positive Zahlen definiert. Wenn Sie eine Zahl mit 10 multiplizieren, erhöhen Sie deren Logarithmus um 1; wenn Sie eine Zahl durch 10 dividieren, verringern Sie deren Logarithmus um 1.
Syntax
LOGTEN(Zahl)
Geben Sie für Zahl den Wert oder die Spalte mit den Werten an. Minitab berechnet den Wert x so, dass 10x = Zahl ist. Wenn Sie „0“ oder eine negative Zahl eingeben, speichert Minitab das Symbol für einen fehlenden Wert (*).
Beispiel
| Rechnerausdruck | Ergebnis |
|---|---|
| LOGTEN(1000) | 4 |
Verwendungen
- Erzwingen einer normaleren Verteilung für positiv schiefe Daten
- Erklären der Krümmung in einem linearen Modell
- Stabilisieren der Streuung innerhalb von Gruppen
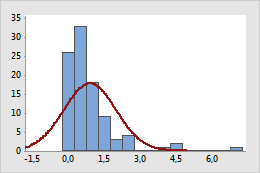
Original
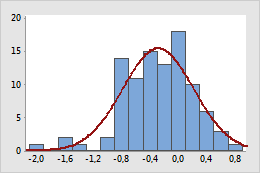
Transformation mit Log10
Beispiel für die Transformation von Daten, um eine normalere Verteilung zu erzielen
In der ursprünglichen Grafik sind die Daten positiv schief, wie durch die Werte außen am rechten (oberen) Randbereich deutlich wird. Die Log10-Transformation komprimiert den oberen Randbereich und streckt den unteren Randbereich, wodurch die transformierten Daten normaler verteilt erscheinen.
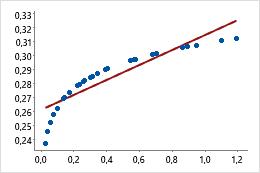
Original
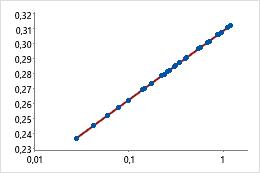
Transformation mit Log10
Beispiel für die Transformation von Daten, um die Krümmung in einem linearen Modell zu erklären
Mit der Linie der einfachen Regression im ursprünglichen Streudiagramm wird die Krümmung der Daten nicht genau modelliert. Nachdem die x-Skala mit Log10 transformiert wurde, liegen die Daten entlang der Linie der einfachen Regression.
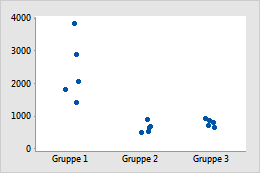
Original
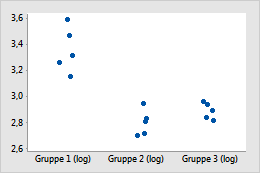
Transformation mit Log10
Beispiel für die Transformation von Daten zum Stabilisieren der Streuung innerhalb von Gruppen
Im ursprünglichen Einzelwertdiagramm enthält Gruppe 1 größere Werte und scheint daher die größere Streuung innerhalb der Gruppe aufzuweisen. Nach der Transformation der Daten erscheinen die Streuungen innerhalb der Gruppen ähnlich.
