Um diese Funktionen zu verwenden, wählen Sie aus.
Die Funktionen „Gamma“, „Unvollständiges Gamma“ und „Natürlicher Logarithmus von Gamma“ erweitern die Fakultätsfunktion (1 * 2 * 3...* n), so dass die Fakultäten sowohl für positive ganze Zahlen als auch für Dezimalzahlen berechnet werden können. Die Funktion „Natürlicher Logarithmus von Gamma“ wird gelegentlich in Berechnungen anstelle der-Funktion „Gamma“ verwendet, da der „Natürliche Logarithmus von Gamma“ mit geringerer Wahrscheinlichkeit sehr große Zahlen erzeugt, die die Speicherkapazität übersteigen und zu einem Überlauf führen.
Syntax
- GAMMA(Form)
- IGAMMA(Grenze,Form)
- LNGAMMA(Form)
Geben Sie für Form die Zahl an, auf die Sie die Funktion anwenden möchten. Geben Sie für Grenze den oberen Grenzwert des Integrals an.
Beispiele
| Rechnerausdruck | Ergebnis |
|---|---|
| GAMMA(0.5) | 1,77245 |
| IGAMMA(1,2) | 0,264241 |
| LNGAMMA(3.5) | 1,20097 |
Formeln
, wird auch als verallgemeinerte Fakultätsfunktion bezeichnet. Sie wird wie folgt definiert:
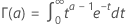
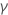, ist eine Variation der vollständigen Gamma-Funktion, die durch ein Integral mit einer endlichen anstatt einer unendlichen Obergrenze definiert ist. Für eine bestimmte Zahl a und eine Obergrenze x gilt Folgendes:
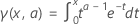
Die Funktion „Natürlicher Logarithmus von Gamma“, 
, entspricht dem natürlichen Logarithmus der vollständigen Gamma-Funktion.
Hinweis
Die Funktion „Vollständiges Gamma“ ist nicht definiert, wenn die Variable a eine negative ganze Zahl oder null ist. Die Funktion „Unvollständiges Gamma“ ist nicht definiert, wenn die Variable a eine negative Zahl oder null ist. Minitab gibt einen fehlenden Wert (*) zurück, wenn die Gamma-Funktion einer Zahl nicht definiert ist.
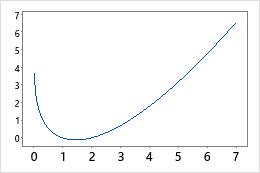
Funktion LNGAMMA
Der „Natürliche Logarithmus von Gamma“ bildet eine konvexe Funktion, die nur für positive Zahlen definiert ist.
Verwendungen
Die Funktion „Gamma“ ist wichtig in der grundlegenden und angewandten Mathematik, Wissenschaft und Technik, u. a. in Anwendungen mit Wärmeleitung in Lasern und menschlichen Geweben. In der Statistik werden mit Hilfe der Funktion „Gamma“ die Dichtefunktion und die kumulative Verteilungsfunktion der Gamma-Verteilung berechnet, mit denen Daten mit positiver Schiefe beschrieben werden können.
