Methods and formulas for goodness-of-fit statistics in Fit Regression Model and Linear Regression

Select the method or formula of your choice.

In This Topic

S
R-sq
R-sq (adj)
R-sq (pred)
PRESS
Test S
Test R-sq
K-fold S
K-fold R-sq
K-fold stepwise R-sq
Log-likelihood
AICc (Akaike's Corrected Information Criterion)
BIC (Bayesian Information Criterion)
Mallows' Cp

S

Notation

Term	Description
MSE	mean square error

R-sq

R² is also known as the coefficient of determination.

Formula

Notation

Term	Description
y_i	i ^th observed response value
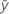	mean response
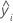	i ^th fitted response

R-sq (adj)

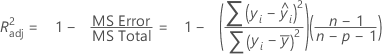
While the calculations for adjusted R² can produce negative values, Minitab displays zero for these cases.

Notation

Term	Description
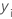	i^th observed response value
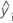	i^th fitted response
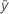	mean response
n	number of observations
p	number of terms in the model

R-sq (pred)

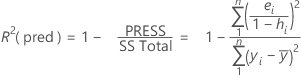
While the calculations for R²(pred) can produce negative values, Minitab displays zero for these cases.

Notation

Term	Description
y_i	i ^th observed response value
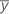	mean response
n	number of observations
e_i	i ^th residual
h_i	i ^th diagonal element of X(X'X)^–1X'
X	design matrix

PRESS

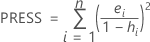
Assesses your model's predictive ability and is calculated as:

Notation

Term	Description
n	number of observations
e_i	i^th residual
h_i	i^th diagonal element of X (X' X)^-1X'

Term

Description

number of observations

e_i

i^th residual

h_i

i^th diagonal element of

X (X' X)^-1X'

Test S

Test S summarizes the distance between the data values and the fitted values in the test data set. Test S is measured in the units of the response.

Formula

where

For regression,

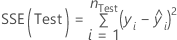
and for weighted regression

Notation

Term	Description
	number of rows in the test data set
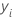	i^th observed response value in the test data set
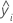	i^th fitted value for the response in the test data set
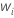	weight for the i^th observation in the test data set

Test R-sq

Test R² is the percentage of variation in the response variable of the test data set that the model explains. The value of test R² ranges between 0% and 100%. (While the calculations for test R² can produce negative values, Minitab Statistical Software displays 0 for these cases.)

Formula

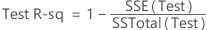
where for regression

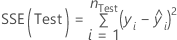
and for weighted regression

The formula for the total sums of squares also depends on whether the data include weights. For regression,

and for weighted regression

where

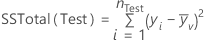
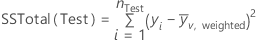
Notation

Term	Description
	number of rows in the test data set
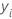	i^th observed response value in the test data set
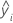	i^th fitted value for the response in the test data set
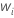	weight for the i^th observation in the test data set
	mean of the response for the test data set
	weighted mean of the response for the test data set

K-fold S

K-fold S summarizes the distance between the data values and the fitted values in the test data set. K-fold S is measured in the units of the response.

Formula

where

For regression,

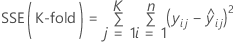
and for weighted regression

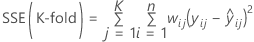Notation

Term	Description
	number of rows in fold j
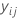	i^th observed response value in fold j
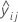	i^th cross-validated fitted value for the response in fold j
K	number of folds
w_i	weight for the i^th observation in fold j

K-fold R-sq

K-fold R² is the percentage of variation in the response variable of the data folds that the model explains. The value of K-fold R² ranges between 0% and 100%. (While the calculations for K-fold R² can produce negative values, Minitab Statistical Software displays 0 for these cases.)

Formula

Minitab calculates the sum of squares for error for each fold. These calculations use the same model terms for every fold, but the estimates of the coefficients can differ. To calculate the k-fold R² statistic, sum the sums of squares for error from the different folds. For regression

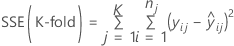
and for weighted regression

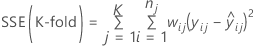Then, the following formula gives the equation for k-fold R²:

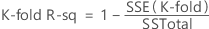
Notation

Term	Description
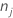	number of rows without missing values for the response or missing values for the predictors that form the candidate terms in the model
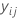	i^th observed response value in fold j
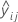	i^th cross-validated fitted value for the response in fold j
K	number of folds
w_ij	weight for the i^th observation in fold j
SSTotal	total sum of squares for all of the data

K-fold stepwise R-sq

K-fold stepwise R-sq evaluates the number of terms in a model from a set of candidate terms. Minitab displays negative values for k-fold stepwise R-sq when they occur.

Formula

Minitab calculate k-fold stepwise R-sq when the stepwise selection method is forward selection with validation and the validation method is k-fold cross-validation. Minitab performs forward selection K times, omitting the data for each fold once. The model for each fold can be different. Once the forward selection procedures are complete, Minitab sums the squared errors for all folds at each step. Minitab uses this sum to calculate k-fold stepwise R-sq. For regression:

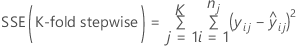
and for weighted regression:

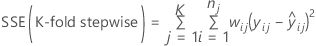
Then, the following formula gives the k-fold stepwise R² value for a step.

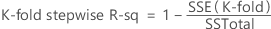
Notation

Term	Description
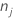	number of rows without missing values for the response or missing values for the predictors that form the candidate terms in the model
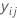	i^th observed response value in fold j
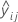	i^th cross-validated fitted value for the response in fold j
K	number of folds
w_ij	weight for the i^th observation in fold j
SSTotal	total sum of squares for all of the data

Log-likelihood

For unweighted analyses, Minitab uses the following equation:

For an analysis that has weights for the observations, Minitab uses the following equation:

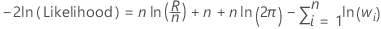
Observations with weights of 0 are not in the analysis.

Notation

Term	Description
n	the number of observations
R	the sum of squares for error for the model
w_i	the weight of the i^th observation

AICc (Akaike's Corrected Information Criterion)

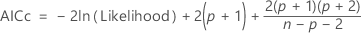
AICc is not calculated when .

Notation

Term	Description
n	the number of observations
p	the number of coefficients in the model, including the constant

BIC (Bayesian Information Criterion)

Notation

Term	Description
p	the number of coefficients in the model, including the constant
n	the number of observations

Mallows' Cp

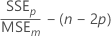
Notation

Term	Description
SSE_p	sum of squared errors for the model under consideration
MSE_m	mean square error for the model with all candidate terms
n	number of observations
p	number of terms in the model, including the constant