In This Topic
Fit
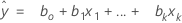
Notation
| Term | Description |
|---|---|
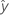 | fitted value |
| xk | kth term. Each term can be a single predictor, a polynomial term, or an interaction term. |
| bk | estimate of kth regression coefficient |
Standard error of fitted value (SE Fit)
The standard error of the fitted value in a regression model with one predictor is:

The standard error of the fitted value in a regression model with more than one predictor is:

For weighted regression, include the weight matrix in the equation:

When the data have a test data set or K-fold cross validation, the formulas are the same. The value of s2 is from the training data. The design matrix and the weight matrix are also from the training data.
Notation
| Term | Description |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | ith predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x'0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Confidence interval for a fitted value (CI)
Formula
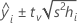
For weighted regression, the formula includes the weights:
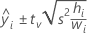
where tv is the 1–α/2 quantile of the t distribution with v degrees of freedom for a two-sided interval. For a 1-sided bound, tv is the 1–α quantile of the t distribution with v degrees of freedom.
When you use a test data set or k-fold cross-validation, the degrees of freedom and the mean square error are from the training data set.
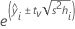
Notation
| Term | Description |
|---|---|
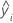 | fitted value |
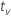 | quantile from the t distribution |
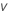 | degrees of freedom |
 | mean square error |
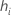 | leverage for the ith observation |
| wi | weight for the ith observation |
Residuals
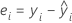
Notation
| Term | Description |
|---|---|
| yi | ith observed response value |
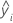 | ith fitted value for the response |
Standardized residual (Std Resid)
Standardized residuals are also called "internally Studentized residuals."
Formula

Notation
| Term | Description |
|---|---|
| ei | i th residual |
| hi | i th diagonal element of X(X'X)–1X' |
| s2 | mean square error |
| X | design matrix |
| X' | transpose of the design matrix |
Standardized residual (Std Resid) with validation
Formula

For weighted regression, the formula includes the weight:
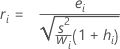
Notation
| Term | Description |
|---|---|
| ei | i th residual in the validation data set |
| hi | leverage for the ith validation row |
| s2 | mean square error for the training data set |
| wi | weight for the ith observation in the validation data set |
Deleted (Studentized) residuals
Also called the externally Studentized residuals. The formula is:
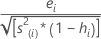
Another presentation of this formula is:

The model that estimates the ith observation omits the ith observation from the data set. Therefore, the ith observation cannot influence the estimate. Each deleted residual has a student's t-distribution with 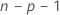 degrees of freedom.
degrees of freedom.
Notation
| Term | Description |
|---|---|
| ei | ith residual |
| s(i)2 | mean square error calculated without the ith observation |
| hi | i th diagonal element of X(X'X)–1X' |
| n | number of observations |
| p | number of terms, including the constant |
| SSE | sum of squares for error |
