Minitab®  Support

Example of Random Forests® Classification

Learn more about
Note

This command is available with the Predictive Analytics Module. Click here for more information about how to activate the module.

A team of researchers collects and publishes detailed information about factors that affect heart disease. Variables include age, sex, cholesterol levels, maximum heart rate, and more. This example is based on a public data set that gives detailed information about heart disease. The original data are from archive.ics.uci.edu.

After initial exploration with CART® Classification to identify the important predictors, the researchers use both TreeNet® Classification and Random Forests® Classification to create more intensive models from the same data set. The researchers compare the model summary table and the ROC plot from the results to evaluate which model provides a better prediction outcome. For results from the other analyses, go to Example of CART® Classification and Example of Fit Model with TreeNet® Classification.

  1. Open the sample data, HeartDiseaseBinary.mtw.
  2. Choose Predictive Analytics Module > Random Forests® Classification.
  3. From the drop-down list, select Binary response.
  4. In Response, enter Heart Disease.
  5. In Response event, select Yes to indicate that heart disease has been identified in the patient.
  6. In Continuous predictors, enter Age, Rest Blood Pressure, Cholesterol, Max Heart Rate, and Old Peak.
  7. In Categorical predictors, enter Sex, Chest Pain Type, Fasting Blood Sugar, Rest ECG, Exercise Angina, Slope, Major Vessels, and Thal.
  8. Click OK.

Interpret the results

For this analysis, the number of observations is 303. Each of the 300 bootstrap samples uses the 303 observations to create a tree. The data includes a good split of nonevents and events.

Random Forests® Classification: Heart Diseas vs Age, Rest Blood P, ...

Method Model validation Validation with out-of-bag data Number of bootstrap samples 300 Sample size Same as training data size of 303 Number of predictors selected for node splitting Square root of the total number of predictors = 3 Minimum internal node size 2 Rows used 303
Binary Response Information Variable Class Count % Heart Disease Yes (Event) 139 45.87 No 164 54.13 All 303 100.00

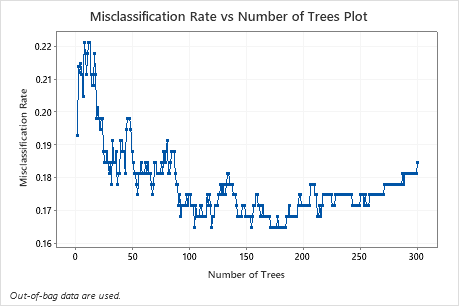
The Misclassification Rate vs Number of Trees Plot shows the entire curve over the number of trees grown. The misclassification rate is approximately 0.18.

Random Forests® Classification: Heart Diseas vs Age, Rest Blood P, ...

Model Summary Total predictors 13 Important predictors 13 Statistics Out-of-Bag Average -loglikelihood 0.4004 Area under ROC curve 0.9028 95% CI (0.8693, 0.9363) Lift 2.1079 Misclassification rate 0.1848

TreeNet® Classification: Heart Diseas vs Age, Rest Blood P, Cholesterol, ...

Model Summary Total predictors 13 Important predictors 13 Number of trees grown 500 Optimal number of trees 351 Statistics Training Test Average -loglikelihood 0.2341 0.3865 Area under ROC curve 0.9825 0.9089 95% CI (0.9706, 0.9945) (0.8757, 0.9421) Lift 2.1799 2.1087 Misclassification rate 0.0759 0.1750

The Model summary table shows that the average negative loglikelihood is 0.3994. These statistics indicate a similar model to what TreeNet® Classification creates when growing 500 trees. Also, the misclassification rates are similar.

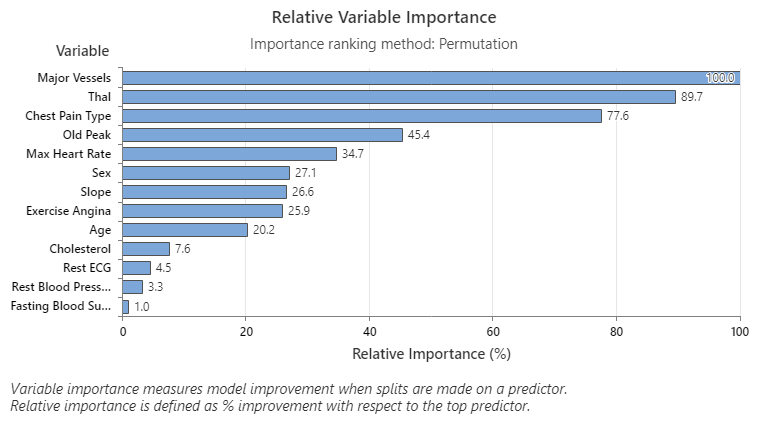
The Relative Variable Importance graph plots the predictors in order of their effect on model improvement when splits are made on a predictor over the sequence of trees. The most important predictor variable is Major Vessels. If the contribution of the top predictor variable, Major Vessels, is 100%, then the next important variable, Thal, has a contribution of 89.7%. This means Thal is 89.7% as important as Major Vessels in this classification model.

Random Forests® Classification: Heart Diseas vs Age, Rest Blood P, ...

Confusion Matrix Predicted Class (Out-of-Bag) Actual Class Count Yes No % Correct Yes (Event) 139 109 30 78.42 No 164 26 138 84.15 All 303 135 168 81.52 Out-of-Bag Statistics (%) True positive rate (sensitivity or power) 78.42 False positive rate (type I error) 15.85 False negative rate (type II error) 21.58 True negative rate (specificity) 84.15

The confusion matrix shows how well the model separates the classes correctly. In this example, the probability that an event is predicted correctly is 78.42%. The probability that a nonevent is predicted correctly is 84.15%.

Random Forests® Classification: Heart Diseas vs Age, Rest Blood P, ...

Misclassification Out-of-Bag Actual Class Count Misclassed % Error Yes (Event) 139 30 21.58 No 164 26 15.85 All 303 56 18.48

The misclassification rate helps indicate whether the model will predict new observations accurately. For prediction of events, the misclassification error is 21.58%. For the prediction of nonevents, the misclassification error is 15.85% and for overall, the misclassification error is 18.48%.

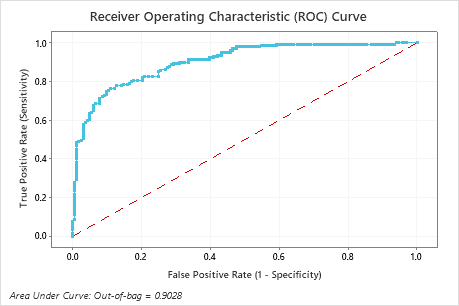
The area under the ROC curve for these data is approximately 0.9028, which shows a slight improvement over the CART® Classification model. The TreeNet® Classification model has a test AUROC of 0.9089, so these 2 methods give similar results.

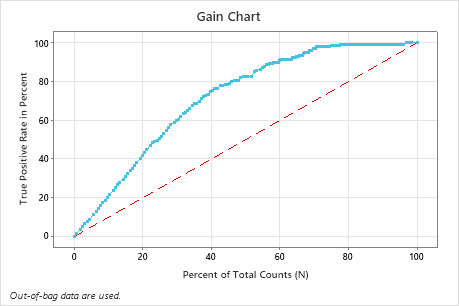
In this example, the gain chart shows a sharp increase above the reference line, then a flattening. In this case, approximately 40% of the data account for approximately 78% of the true positives. This difference is the extra gain from using the model.

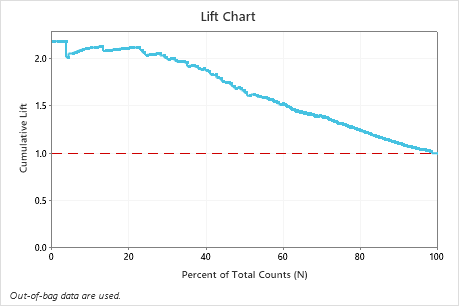
In this example, the lift chart shows a large increase above the reference line that gradually drops off.

Copyright © 2024 Minitab, LLC. All rights Reserved.