In This Topic
Z.LSL, Z.USL, and Z.Bench for potential (within) capability
Benchmark Z statistics for potential capability are calculated by finding the Z value using the standard normal (0,1) distribution for the corresponding statistics.
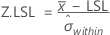

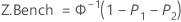
where:


Notation
| Term | Description |
|---|---|
| Φ (X) | Cumulative distribution function (CDF) of a standard normal distribution |
| Φ-1 (X) | Inverse CDF of a standard normal distribution |
 | Within-subgroup standard deviation |
Confidence intervals for Z.bench for a process with two specification limits
Two-sided interval


where
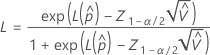
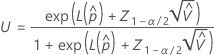
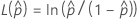
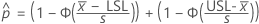
To calculate  , substitute the sample estimates for the parameters in the formula for
, substitute the sample estimates for the parameters in the formula for 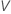 :
:



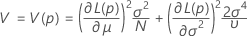
where
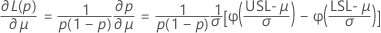

One-sided upper confidence bound
To calculate a one-sided upper confidence bound, change 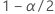 to
to  in the definition of U.
in the definition of U.
Notation
| Term | Description |
|---|---|
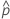 | the estimated tail probabilities outside of the specificataion limits |
 | the (1 - α / 2)th percentile of the standard normal distribution |
| α | the alpha for the confidence level |
 | the process mean (estimated from the sample date or a historical value) |
| s | the sample standard deviation within subgroups |
| υ | the degrees of freedom for s |
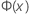 | the Cumulative Distribution Function (CDF) from a standard normal distribution |
 | the Probability Density Function (PDF) from a standard normal distribution |
| USL | the upper specification limit |
| LSL | the lower specification limit |
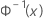 | the inverse CDF from a standard normal distribution |
Confidence intervals for Z.bench for a process with one specification limit
The calculations for the confidence interval for Z.Bench depend on which specification limit the process has.
Lower specification limit, two-sided confidence interval
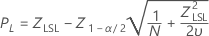
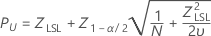

Lower specification limit, one-sided confidence bound

Minitab solves the following equation to find p1:
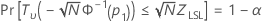
where

Upper specification limit, two-sided confidence interval
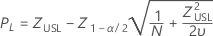
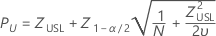

Upper specification limit, one-sided confidence bound

Minitab solves the following equation to find p2:
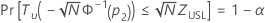
where

Notation
| Term | Description |
|---|---|
| LSL | the lower specification limit |
| USL | the upper specification limit |
| α | the alpha for the confidence level |
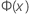 | the Cumulative Distribution Function (CDF) from a standard normal distribution |
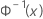 | the inverse CDF from a standard normal distribution |
 | the (1 - α/2)th percentile of the standard normal distribution |
| N | the total number of measurements |
| υ | the degrees of freedom for s |
 | the process mean (estimated from the sample date or a historical value) |
| s | the sample standard deviation within subgroups |
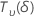 | a random variable that is distributed as a non-central t distribution with  degrees of freedom and non-centrality parameter δ degrees of freedom and non-centrality parameter δ |
