Mean
The mean describes the sample with a single value that represents the center of the data. The mean is calculated as the average of the data, which is the sum of all the observations divided by the number of observations.
N
The sample size (N) is the total number of observations in the sample.
Interpretation
The sample size affects the power of the test.
Usually, a larger sample size gives the test more power to detect a difference between your sample data and the normal distribution. That is, when a difference truly exists, you have a greater chance of detecting it with a larger sample size.
StDev
The standard deviation is the most common measure of dispersion, or how spread out the data are from the mean. A larger sample standard deviation indicates that your data are spread more widely around the mean.
AD
The Anderson-Darling goodness-of-fit statistic (AD) measures the area between the fitted line (based on the normal distribution) and the empirical distribution function (which is based on the data points). The Anderson-Darling statistic is a squared distance that is weighted more heavily in the tails of the distribution.
Interpretation
Minitab uses the Anderson-Darling statistic to calculate the p-value. The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis. Larger values for the Anderson-Darling statistic indicate that the data do not follow the normal distribution.
KS
The Kolmogorov-Smirnov test compares the ECDF (empirical cumulative distribution function) of your sample data with the distribution expected if the data were normal.
Interpretation
Minitab uses the Kolmogorov-Smirnov statistic to calculate the p-value. The p-value is the probability of obtaining a test statistic (such as the Kolmogorov-Smirnov statistic) that is at least as extreme as the value that is calculated from the sample, when the data are normal. Larger values for the Kolmogorov-Smirnov statistic indicate that the data do not follow the normal distribution.
RJ
The Ryan-Joiner statistic measures how well the data follow a normal distribution by calculating the correlation between your data and the normal scores of your data. If the correlation coefficient is near 1, the population is likely to be normal. This test is similar to the Shapiro-Wilk normality test.
Interpretation
Minitab uses the Ryan-Joiner statistic to calculate the p-value. The p-value is the probability of obtaining a test statistic (such as the Ryan-Joiner statistic) that is at least as extreme as the value that is calculated from the sample, when the data are normal. Larger values for the Ryan-Joiner statistic indicate that the data do not follow the normal distribution.
P-Value
The p-value is a probability that measures the evidence against the null hypothesis. A smaller p-value provides stronger evidence against the null hypothesis.
Interpretation
Use the p-value to determine whether the data do not follow a normal distribution.
- P-value ≤ α: The data do not follow a normal distribution (Reject H0)
- If the p-value is less than or equal to the significance level, the decision is to reject the null hypothesis and conclude that your data do not follow a normal distribution.
- P-value > α: You cannot conclude that the data do not follow a normal distribution (Fail to reject H0)
- If the p-value is larger than the significance level, the decision is to fail to reject the null hypothesis. You do not have enough evidence to conclude that your data do not follow a normal distribution.
Probability Plot
A probability plot creates an estimated cumulative distribution function (CDF) from your sample by plotting the value of each observation against the observation's estimated cumulative probability.
Interpretation
Use a probability plot to visualize how well your data fit the normal distribution.
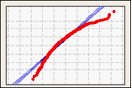
Right-skewed data
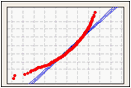
Left-skewed data
Tip
In Minitab, hold your pointer over the fitted distribution line to see a chart of percentiles and values.
