Box-Cox transformation
The Box-Cox transformation estimates a lambda value, as shown in the following table, which minimizes the standard deviation of a standardized transformed variable. The resulting transformation is Yλ when λ ҂ 0 and ln Y when λ = 0.
The Box-Cox method searches through many types of transformations. The following table shows some common transformations where Y' is the transform of the data Y.
| Lambda (λ) value | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
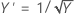 |
 |
 |
Algorithm for Johnson transformation
The Johnson transformation optimally selects one of three families of distribution to transform the data to follow a normal distribution.
| Johnson family | Transformation function | Range |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , where
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
The algorithm uses the following procedure:
- Considers almost all potential transformation functions from the Johnson system.
- Estimates the parameters in the function using the method described in Chou, et al.1
- Transforms the data using the transformation function.
- Calculates Anderson-Darling statistics and the corresponding p-value for the transformed data.
- Selects the transformation function that has the largest p-value that is greater than the p-value criterion (default is 0.10) that you specify in the Transform dialog box. Otherwise, no transformation is appropriate.
Notation
| Term | Description |
|---|---|
| SB | The Johnson family distribution with the variable bounded (B) |
| SL | The Johnson family distribution with the variable lognormal (L) |
| SU | The Johnson family distribution with the variable unbounded (U) |
For more information on the Johnson transformation, see Chou, et al.1 Minitab replaces the Shapiro-Wilks normality test used in that text with the Anderson-Darling test.
For information on the probability plot, percentiles, and their confidence intervals, go to Methods and formulas for distributions in Individual Distribution Identification.
