Fisher 精确检验
Fisher 精确检验可以检验独立性。该检验以精确分布(而不是用于 Pearson 和似然比检验的近似卡方分布)为基础。当预期单元格计数较小且卡方近似不佳时,可以使用 Fisher 精确检验。
公式
- 总体大小
- 总观测值数
- 总体中的成功次数
- 第 1 行中的观测值数
- 样本数量
- 第 1 列中的观测值数
示例
| 儿童 | 成人 | 行合计 | |
|---|---|---|---|
| 糖 | 9 | 1 | 10 |
| 巧克力片 | 2 | 8 | 10 |
| 列合计 | 11 | 9 | 20 |
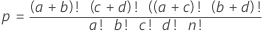
| 儿童 | 成人 | 行合计 | |
|---|---|---|---|
| 糖 | a | b | a+b |
| 巧克力片 | c | d | c+d |
| 列合计 | a+c | b+d | a+b+c+d |
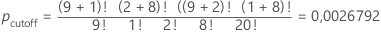
对于此示例,小于或等于其他可能矩阵 pcutoff 的 p 值的和为 0.0054775。
McNemar 精确检验
McNemar 检验可比较处理前和处理后实测的比率。例如,您可以使用 McNemar 检验确定培训计划是否会更改正确回答问题的参与者的比率。
McNemar 检验的观测值可以汇总到 2 x 2 表格中,如下所示。
| 处理后 | |||
| 处理前 | 条件成立 | 条件不成立 | 合计 |
| 条件成立 | n11 | n12 | n1. |
| 条件不成立 | n21 | n22 | n2. |
| 合计 | n·1 | n·2 | n·· |
培训示例的条件是正确答案。因此,n21 表示培训后(而不是培训前)正确回答问题的参与者数量。n12 表示培训前(而不是培训后)正确回答问题的参与者数量。参与者总数用 n.. 表示。
估计的差值
用 δ 表示总体中边际概率之间的差值,p1.- p.1。估计的差值  ,可通过以下公式得出:
,可通过以下公式得出:
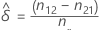
置信区间
通过以下公式得出近似 100(1 – α)% 的置信区间:

其中,α 是检验的显著性水平,z α/2 是与 α/2 的尾概率关联的 z 分值,SE 可通过以下公式得出:
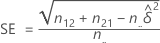
P 值
原假设为 δ = 0。原假设检验的精确 p 值的计算公式为:

其中,X 是随机变量,来自事件概率为 0.5 且试验数等于 n21 + n12 的二项分布。
Cochran-Mantel-Haenszel 检验
该检验假设不存在三因子交互作用。该检验的目的是在控制多余变量的同时评估两个二分法变量之间的相关度。可以使用自由度为 1 的卡方百分位数比较 CMH 统计量。
Cochran-Mantel-Haenszel (CMH) 检验仅适用于存在三个或更多分类变量且前两个变量各有两个水平的情况。为了执行 CMH 检验,会将前两个变量之外的所有变量视为单个变量 Z,并将每个水平组合视为 Z 的一个水平。
公式
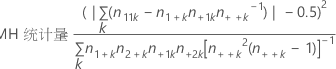
表示法
| 项 | 说明 |
|---|---|
| k | Z 的水平 |
| n11k | 第 1 行、第 1 列中的观测值数 |
| n1+k | 第 1 行中的观测值数 |
| n+1k | 第 1 列中的观测值数 |
| n++k | 观测值总数 |
| n2+k | 第 2 行中的观测值数 |
| n+2k | 第 2 列中的观测值数 |
