请选择您所选的方法或公式。
每个类别的预期值
公式
每个类别 i 的预期值 E 的计算公式为:
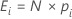
表示法
| 项 | 说明 |
|---|---|
| pi | 第 i 个类别的检验比率,等于 1/k 或您提供的值 |
| k | 可区分类别数 |
| N | 总实测值 (O1 + ... + Ok) |
| Oi | 第 i 个类别的实测值 |
卡方检验统计量
公式
卡方检验统计量的计算公式为:
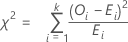
表示法
| 项 | 说明 |
|---|---|
| k | 可区分类别数 |
| Oi | 第 i 个类别的实测值 |
| Ei | 第 i 个类别的预期值 |
卡方统计量的贡献
公式
卡方值的第 i 个类别的贡献为:

表示法
| 项 | 说明 |
|---|---|
| Oi | 第 i 个类别的实测值 |
| Ei | 第 i 个类别的预期值 |
自由度 (DF)
公式
自由度 (DF) 的计算公式为:

表示法
| 项 | 说明 |
|---|---|
| 自由度 | 自由度 |
| k | 类别数 |
P 值
公式
p 值的计算公式为:Prob (Χ > 检验统计量)
表示法
| 项 | 说明 |
|---|---|
| X | 服从自由度为 k – 1 的卡方分布 |
计算示例
已指定:
| 类别 i | 实测的 Oi | 检验比率 pi |
|---|---|---|
| A | 5 | 0.1 |
| B | 15 | 0.2 |
| C | 10 | 0.3 |
| D | 10 | 0.4 |
| N=40 |
已计算:
| 类别 i | 预期值
Ei = (pi * N) |
对卡方的贡献
(Oi- Ei)2 / Ei |
|---|---|---|
| A | 0.1 * 40 = 4 | (5 – 4)2 / 4 = 0.25 |
| B | 0.2 * 40 = 8 | (15 – 8)2 / 8 = 6.125 |
| C | 0.3 * 40 = 12 | (10 – 12)2 / 12 = 0.3333 |
| D | 0.4 * 40 = 16 | (10 – 16)2 / 16 = 2.25 |
χ2 = 0.2500 + 6.1250 + 2.2500 + 0.3333 = 8.9583
自由度 = k – 1 = 3
p 值 = Prob (Χ > 8.9583) = 0.0299
表示法
| 项 | 说明 |
|---|---|
| 自由度 | 自由度 |
| k | 类别数 |
