请选择您所选的方法或公式。
均值(正态)
标准差是已知的
当总体标准差是已知时,来自正态分布的均值的置信区间为:

边际误差为 
为 n 求解:

标准差是未知的
当总体标准差是未知时,来自正态分布的均值的置信区间为:
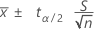
边际误差为 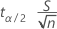
要为 n 求解,请计算最小 n,以便:
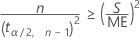
表示法
| 项 | 说明 |
|---|---|
 | 样本均值 |
| zα/2 | 标准正态分布在 1- α /2 处的反向累积概率;α = 1 - 置信水平/100 |
| σ | 总体标准差(假定已知) |
| n | 样本数量 |
| ME | 边际误差 |
| t α/2 | 自由度为 n-1 的 t 分布在 1-α/2 处的反向累积概率 |
| S | 计划值 |
比率(二项)
下限
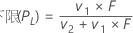
上限
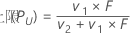
区间 (PL, PU)是p的近似 100(1 – α)%置信区间。
注意
要为 n 求解,请计算最小 n,以便:
(P – PL) ≤ ME 和 (PU – P) ≤ ME其 P =计划值比例。
表示法
| 项 | 说明 |
|---|---|
| v1 (下限) | 2x |
| v2 (下限) | 2(n – x + 1) |
| v1 (上限) | 2(x + 1) |
| v2 (上限) | 2(n – x) |
| x | 事件数 |
| n | 试验数 |
| F (下限) | 具有 v1 和 v2 自由度的下 α/2 点 F 分布 |
| F (上限) | 上 v1 和 v2 自由度的下 α/2 点 F 分布 |
率和均值 (Poisson)
公式
来自 Poisson 分布的率或均值的置信下限为:
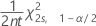
来自 Poisson 分布的率或均值的置信上限为:
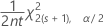
边际误差的下限等于 −1 ×(置信下限)。边际误差的上限等于置信上限。
要为 n 求解,请计算最小 n,以便:
(S – SL) ≤ ME 且 (SU – S) ≤ ME
表示法
| 项 | 说明 |
|---|---|
| n | 样本数量 |
| t | 观测值长度;对于 Poisson 均值,长度 = 1 |
| s | Poisson 过程中的总发生次数 |
| χ2p, x | 自由度为 p 的卡方分布的第 x 个上百分位点,其中 0 < x < 1 |
| S | 计划值 |
| ME | 边际误差 |
方差和标准差(正态)
公式
来自正态分布的方差的置信下限为:
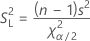
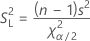
来自正态分布的方差的置信上限为:
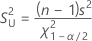
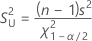
要获得标准差的置信区间,请计算上述等式的平方根。
边际误差的下限等于 −1 ×(置信下限)。边际误差的上限等于置信上限。
要针对方差对 n 求解,请计算最小 n,以便:
(S2 – S2L) ≤ ME 且 (S2U – S2) ≤ ME
要针对标准差对 n 求解,请计算最小 n,以便:
(S – SL) ≤ ME 且 (SU – S) ≤ ME
表示法
| 项 | 说明 |
|---|---|
| n | 样本数量 |
| s2 | 样本方差 |
| Χ2 p | 自由度为 (n – 1) 的卡方分布的第 100p 个上百分位点 |
| S | 计划值 |
| ME | 边际误差 |
