显著性水平 (α)
显著性水平(用 alpha 或 α 表示)是 I 型错误风险的最大可接受水平。
解释
使用显著性水平可以确定效应在统计意义上是否显著。由于显著性水平是统计显著性的阈值,因此,值越大,犯 I 型错误的概率越大。I 型错误会错误地得出效应在统计意义上显著的结论。
假定标准差
假定标准差是在重复的试验性游程下响应测量值的标准差。如果您已经在 Minitab 中执行了一个生成方差分析表的分析,则可以使用调整后的误差均方的平方根。
解释
使用假定标准差可以描述数据的变异程度。假定标准差的值越大,数据中的变异性或“噪声”越大,设计的统计功效越低。
因子数
该数值显示设计中有多少个因子。
解释
使用因子数可以验证设计中是否包含您需要研究的所有因子。因子是您在试验中控制的变量。因子又称为独立变量、解释变量和预测变量。对于功效和样本数量计算,所有的因子都是数值。数值因子在试验中只使用少数几个控制值,即使可能存在多个值也是如此。这些值称为因子水平。
例如,您正在研究在制造过程中可能影响塑性强度的因子。您决定在试验中包括温度。因为温度是因子,所以试验中仅包含三个温度设置:100 °C、150 °C 和 200 °C。
设计
该数值显示一个仿行中有多少个中心点。
解释
使用此数值可以确定在功效计算过程中使用的 Plackett-Burman 设计。角点是因子在其处位于高水平或低水平的试验性游程。
中心点数
该数值显示设计中有多少个中心点。
解释
使用中心点数可以查看不同的中心点数对结果的效应。中心点是所有因子都设置在低设置和高设置之间中间位置的游程。
当设计中包括角点的仿行时,中心点对结果产生的影响通常较小。中心点除了会影响功效计算外,还有其他用途。例如,对响应中的弯曲进行检验需要使用中心点。
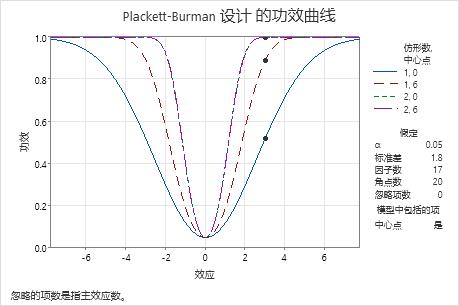
在这些结果中,功效曲线上的点显示差值为 3 时的计算值。具有 1 个仿行和 0 个中心点的设计具有接近 0.5 的功效。具有 1 个仿行和 6 个中心点的设计具有将近 0.9 的功效。有两个仿行时,在图形上很难分辨出针对 0 个中心点的功效曲线和针对 6 个中心点的功效曲线。对于非零效应来说,针对 6 个中心点的曲线稍高些。功效值均接近 1。
方法
| 因子: | 17 | 设计: | 20 |
|---|
结果
| 中心点 | 效应 | 仿行数 | 总试验数 | 功效 |
|---|---|---|---|---|
| 0 | 3 | 1 | 20 | 0.517308 |
| 0 | 3 | 2 | 40 | 0.998927 |
| 6 | 3 | 1 | 26 | 0.889603 |
| 6 | 3 | 2 | 46 | 0.999082 |
效应
如果您输入仿行数、功效值和中心点数,Minitab 将计算效应。效应是您希望设计检测的高因子水平下的响应与低因子水平下的响应之间的差值。此差值是由一个因子单独引起的(主效应)。
解释
使用效应大小可以确定设计对效应的检测能力。如果您输入一个仿行数、一个功效和一个中心点数,Minitab 将计算设计使用指定功效能够检测到的最小效应大小。通常,仿行越多,所设计的试验能够检测到的效应越小。
在这些结果中,具有一个仿行的设计在 80% 功效下能够检测到大约 0.015 的差值。该设计在 90% 功效下可以检测到的差值大约为 0.018(大于 0.015)。具有 2 个仿行的设计在 80% 功效下能够检测到的差值大约为 0.007(小于 0.015)。
方法
| 因子: | 31 | 设计: | 32 |
|---|---|---|---|
| 中心点(合计): | 4 |
结果
| 中心点 | 仿行数 | 总试验数 | 功效 | 效应 |
|---|---|---|---|---|
| 4 | 1 | 36 | 0.8 | 0.0153027 |
| 4 | 1 | 36 | 0.9 | 0.0180278 |
| 4 | 2 | 68 | 0.8 | 0.0073261 |
| 4 | 2 | 68 | 0.9 | 0.0084775 |
仿行数
仿行是多个具有相同因子设置的试验性游程。
解释
使用仿行数可以估计要在设计中包括多少个试验性游程。如果您输入功效、效应大小和中心点数,Minitab 将计算仿行数。因为仿行数和中心点数是用整数值给定的,所以实际功效可能会大于目标值。 如果增加仿行数,设计的功效也会提高。您希望有足够的仿行以达到足够的功效。
因为仿行数是整数值,所以指定的功效值是目标功效值。实际功效值针对的是设计试验中的仿行数和中心点数。实际功效值至少与目标功效值相等。
在这些结果中,Minitab 计算达到目标功效所需的仿行数。要在 0.8 功效下检测效应 2,设计中需要 1 个仿行。要达到功效 0.9,设计需要 2 个仿行。具有 2 个仿行的设计的实际功效大于 0.99。此实际功效是一个大于或等于 0.9 且可通过使用仿行数整数值获得的最小功效值。要在 0.8 功效下检测较小的效应 0.9,设计需要 4 个仿行。要在 0.9 功效下检测较小的效应 0.9,设计需要 5 个仿行。
方法
| 因子: | 15 | 设计: | 32 |
|---|---|---|---|
| 中心点(合计): | 0 |
结果
| 中心点 | 效应 | 仿行数 | 总试验数 | 目标功效 | 实际功效 |
|---|---|---|---|---|---|
| 0 | 2.0 | 1 | 32 | 0.8 | 0.877445 |
| 0 | 2.0 | 2 | 64 | 0.9 | 0.995974 |
| 0 | 0.9 | 4 | 128 | 0.8 | 0.843529 |
| 0 | 0.9 | 5 | 160 | 0.9 | 0.914018 |
总游程数
试验性游程是在其处度量响应的因子水平组合。总游程数是指设计中有多少个响应测量。在同一因子水平组合下的多次执行被视为单独的试验性游程,也称为仿行。
解释
使用总游程数可以验证设计的试验大小是否适合您的资源。对于 Plackett-Burman 设计,以下公式提供总游程数:
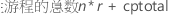
| 项 | 说明 |
|---|---|
| n | 每个仿行的角点数 |
| r | 仿行数 |
| cptotal | 中心点数 |
在这些结果中,具有 12 个角点和 4 个中心点的设计总共有 16 个游程。具有 2 个仿行的设计中的游程数为 12*2 + 4 = 28。
方法
| 因子: | 8 | 设计: | 12 |
|---|---|---|---|
| 中心点(合计): | 4 |
结果
| 中心点 | 效应 | 仿行数 | 总试验数 | 功效 |
|---|---|---|---|---|
| 4 | 2.5 | 1 | 16 | 0.523009 |
| 4 | 2.5 | 2 | 28 | 0.895399 |
功效
设计的功效是设计确定效应在统计意义上显著的概率。效应大小是响应变量在高水平因子下的均值与低水平因子下的均值之间的差值。
解释
使用功效值可以确定设计检测效应的能力。如果您输入仿行数、效应大小和中心点数,Minitab 将计算设计的功效。功效值 0.9 通常被认为已足够。如果值为 0.9,则表示设计检测到指定大小的效应的概率为 90%。通常,仿行数越小,功效越低。如果设计的功效低,您可能无法检测到效应并错误地得出不存在任何效应的结论。
这些结果演示了如何通过增加试验运行次数来提高功效。如果功效大小为 0.9,总运行次数为 64,则设计的功效大约为 0.55。如果总运行次数为 160,则设计的功效可大约提高至 0.91。
这些结果还演示了如何通过增加效应大小来提高功效。如果设计的运行次数为 64,效应大小为 0.9,则功效大约为 0.55。如果效应大小为 1.5,则功效会大约提高至 0.93。
方法
| 因子: | 15 | 设计: | 32 |
|---|---|---|---|
| 中心点(合计): | 0 |
结果
| 中心点 | 效应 | 仿行数 | 总试验数 | 功效 |
|---|---|---|---|---|
| 0 | 1.5 | 5 | 160 | 0.999830 |
| 0 | 1.5 | 2 | 64 | 0.932932 |
| 0 | 0.9 | 5 | 160 | 0.914018 |
| 0 | 0.9 | 2 | 64 | 0.545887 |
功效曲线
此功效曲线描绘了设计的功效与效应大小之间的关系。效应是指因子的高水平响应均值与低水平响应均值之差。
解释
使用功效曲线可以为您的设计评估相应的属性。
功效曲线表示每个中心点与仿行组合的功效和效应大小之间的关系。功效曲线上的每个符号都表示一个基于所输入属性的计算值。例如,如果您输入一个仿行数、一个功效值和一个中心点数,Minitab 会计算相应的效应大小并将计算值显示在相应的仿行与中心点组合图形上。如果您针对仿行或中心点求解,则图上还包括能够达到目标功效组合中的其他仿行与中心点组合的曲线。如果自由度不够大,无法评估统计显著性,则图中不显示曲线。
检查曲线上的值,确定该试验在特定功效值、角点数和中心点数处检测到的效应大小。通常认为功效值为 0.9 足矣。但是,有些从业者认为功效值为 0.8 足矣。如果设计的功效较低,则可能无法检测到实际上有显著意义的效应。增加仿行的数量可以提高设计的功效。您希望设计中有足够多的试验性游程以达到足够大的功效。设计的功效越大,就可以检测到越大的效应。
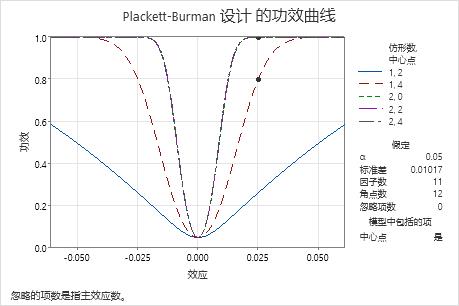
在这些结果中,Minitab 针对效应大小 0.025 计算至少达到 0.8 或 0.9 的目标功效所需的仿行数。在设计的试验中,用 12 个角点研究 11 个因子。计算过程中考虑了具有 0、2 或 4 个中心点的设计试验。显示 1 个仿行和 4 个中心点的曲线上有一个符号,表明效应 0.25 的功效高于目标功效 0.8。表示具有 2 个仿行的试验的 3 条曲线上有一些符号,表明效应 0.025 的检测功效超过目标功效 0.9。
由于一个解有 2 个仿行和 2 个中心点,另一个解有 1 个仿行和 4 个中心点,因此图中还包括一条针对具有 1 个仿行和 2 个中心点的试验的曲线。对于效应 0.025,该试验未实现任一目标功效,因此该曲线上没有符号。图中不包括针对 1 个仿行和 0 个中心点的曲线,这是因为从模型中省略了 0 项后,此试验的自由度不够大,无法评估统计显著性。
