步骤 1:检查计算值
Minitab 使用您为两个功效函数变量输入的值,计算设计的仿行数、主效应均值之间的最大差值或者功效。
- 主效应均值之间的最大差值
- 最大差值是要在具有最高均值的因子水平和具有最低均值的因子水平之间检测到的差异。计算过程中使用具有最高水平的因子来生成对于其他因子来说较为保守的计算结果。Minitab 计算能够由设计检测到的最小差值。仿行越多,设计能够检测到的差值越小。通常,您希望能够检测对于您的应用有实际意义的最小差值。
- 仿行数
- 如果您输入主效应均值之间的最大差值和功效值,Minitab 将计算仿行数。仿行是多个具有相同因子设置的试验性游程。因为仿行数是整数值,所以实际功效可能比目标值稍大。
- 总游程数
- 对于每种情况,Minitab 将根据仿行数计算总游程数。单个仿行中的游程数是水平数的倍数。总游程数是基本设计大小和仿行数的乘积。
- 功效值
- 如果您输入仿行数和主效应均值之间的最大差值,Minitab 将计算功效值。功效是正确发现显著差异的概率。功效值 0.9 通常被视为足矣。如果值为 0.9,则表示在因子设置之间检测到差值的概率为 90%。在其他设计属性保持恒定的情况下,当总游程数较小或者最大值较小时,设计的功效较小。
结果
| 最大差值 | 仿行数 | 总试验数 | 目标功效 | 实际功效 |
|---|---|---|---|---|
| 2.0 | 3 | 108 | 0.8 | 0.932615 |
| 2.0 | 3 | 108 | 0.9 | 0.932615 |
| 1.8 | 3 | 108 | 0.8 | 0.867493 |
| 1.8 | 4 | 144 | 0.9 | 0.952918 |
主要结果:最大差值、仿行数、总游程数、目标功效和实际功效
在这些结果中,Minitab 计算为了达到目标功效 80% 和目标功效 90% 所需的仿行数。要检测差值 2.0,设计中需要有 3 个仿行才能达到目标值 80% 或 90%。具有 2 个仿行的设计的功效小于目标功效 80%。要检测较小的差值 1.8,设计中需要 3 个仿行,在这种情况下所达到的功效将大于 80% 但不超过 90%。要在 90% 功效下检测较小的差值,设计的试验中需要 4 个仿行。因为仿行数是整数值,所以实际功效大于目标功效。
这些结果还显示具有最多水平的因子包含 4 个水平。这些结果对于 4 水平因子非常精确。对于两个 3 水平因子,仿行数可能会有所不同,当实际功效远大于目标功效时尤其如此。
步骤 2:检查功效曲线
使用功效曲线可以为您的设计评估相应的属性。
功效曲线表示对于每个仿行数,功效和最大差值之间的关系。功效曲线上的每个符号都表示一个基于所输入属性的计算值。例如,如果您输入一个仿行数和一个功效值,Minitab 会计算相应的最大差值并将计算值显示在图形上。
检查曲线上的值,为具有最大水平的因子确定该试验在特定功效值和仿行数处检测到的最大均值与最小均值之间的差值。通常认为功效值为 0.9 足矣。但是,有些从业者认为功效值为 0.8 足矣。如果设计的功效较低,则可能无法检测到实际上有显著意义的差值。增加试验性游程的总数可以提高设计的功效。您希望设计中有足够多的试验性游程以达到足够大的功效。设计的功效越大,检测到的差值也越大。
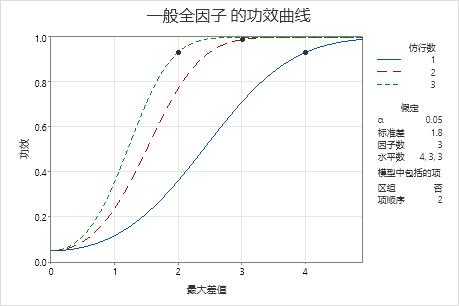
在这些结果中,Minitab 针对最大差值 2、3 或 4 计算至少取得 0.9 的功效所需的仿行数。图中对于每个仿行数都有一条曲线。要使检测到的最大差值为 2、功效值最低为 0.9,设计中需要有 3 个仿行。图中针对 3 个仿行有一条曲线,并在功效超过 0.9 的最大差值 2 处显示一个符号。要使检测到的最大差值为 3、功效值最低为 0.9,设计中需要有 2 个仿行。如果最大差值为 4、最小功效为 0.9,则设计中需要有 1 个仿行。
