α (alpha)
显著性水平(用 alpha 或 α 表示)是在原假设为真时否定原假设(I 型错误)的风险的最大可接受水平。Alpha 还解释为当原假设 (H0) 为真时检验的功效。在分析数据之前通常会选择显著性水平。默认的显著性水平为 0.05。
解释
使用显著性水平可以在原假设 (H0) 为真时最小化检验的功效值。显著性水平越高,检验功效越大,犯 I 型错误(否定原本为真的原假设)的概率越大。
比值
此值表示比较标准差或方差与假设值之间的比值。
解释
Minitab 基于指定的功效和样本数量,计算您能够检测到的最小比值。样本数量越大,能够检测到的比值越小。您希望能够检测对于您的应用有实际意义的最小比值。
使用功效曲线可以更完整地研究在给定功效下样本数量和比值之间的关系。
样本数量
样本数量是样本中的观测值总数。
解释
使用样本数量可以估计在特定差值下,假设检验取得特定功效值所需的观测值个数。
Minitab 计算样本必须为多大,具有指定功效的检验才能检测到指定的比值。因为样本数量是整数,所以检验的实际功效可能比指定的功效值稍大。
样本数量越大,检验功效也会越高。您希望样本中有足够的观测值以达到足够的功效。但是,您不希望样本数量过大,让您在不必要的抽样上浪费时间和金钱或者检测在统计意义上显著但不重要的差值。
使用功效曲线可以更完整地研究在给定功效下样本数量和差值之间的关系。
功效
假设检验的功效是指检验正确否定原假设的概率。假设检验的功效受检验的样本数量、差值、数据变异性和显著性水平的影响。
有关更多信息,请转到什么是功效?。
解释
Minitab 根据指定的比值和样本数量计算检验的功效。功效值 0.9 通常被认为已足够。如果值为 0.9,则表示当差值确实存在时,检测到总体比较标准差或方差与假设标准差或方差之差的概率为 90%。如果检验的功效较低,您可能无法检测到差值并错误地得出不存在任何差值的结论。通常情况下,样本数量越少或比值越接近 1 时,检验检测到差值的功效就越低。
如果您输入检验的比值和功效值,Minitab 将计算样本必须为多大。Minitab 还将计算该样本数量检验的实际功效。因为样本数量是整数,所以检验的实际功效可能比指定的功效值稍大。
注意
在执行基本统计中的单方差时,Minitab 将同时显示卡方方法和 Bonett 方法的输出。但是,在执行单方差的功效和样本数量时,Minitab 仅使用卡方方法。
功效曲线
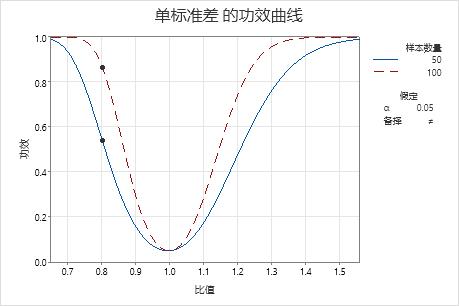
功效曲线描绘了检验的功效与比值之间的关系。
解释
使用功效曲线可以为您的检验评估合适的样本数量或功效。
功效曲线表示当显著性水平保持恒定时,每个样本数量的每个功效与比值组合。功效曲线上的每个符号都表示一个基于输入值的计算值。例如,如果您输入一个样本数量和一个功效值,Minitab 会计算相应的比值并将计算值显示在图形上。
检查曲线上的值,确定可以在特定功效值和样本数量处检测到的比值。通常认为功效值为 0.9 足矣。但是,有些从业者认为功效值为 0.8 足矣。如果假设检验的功效较低,则可能无法检测到实际上有显著意义的比值。如果增加样本数量,检验功效也会提高。您希望样本中有足够的观测值以达到足够的功效。但是,您不希望样本数量过大,让您在不必要的抽样上浪费时间和金钱或者检测在统计意义上显著但不重要的差值。 如果您减小要检测的比值,则功效也会降低。
注意
在执行基本统计中的单方差时,Minitab 将同时显示卡方方法和 Bonett 方法的输出。但是,在执行单方差的功效和样本数量时,Minitab 仅使用卡方方法。
在此图形中,样本数量 50 的功效曲线表明,对于比值 0.8,检验的功效大约为 0.54。样本数量 100 的功效曲线表明,对于比值 0.8,检验的功效大约为 0.87。如果功效 0.87 对于您的情形足够大,则应当收集 100 个样本。如果您需要检测小于 0.8 的比值,则将需要收集更多的样本。