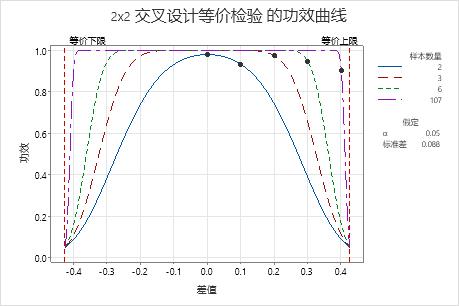
一家消费者保健公司的质量工程师想要确定普通抗酸药与名牌抗酸药是否等价。有两组参与者,在前 5 天他们服用一种抗酸药,接着是两周的清除期,在之后的 5 天服用另一种抗酸药。组 1 先服用普通抗酸药(检验处理),后服用名牌抗酸药(参考处理)。组 2 先服用名牌抗酸药,后服用普通抗酸药。工程师在每次处理的最后一天测量胃部 pH 值。由于 pH 值越低酸性越大,因此值越大表示药物越有效。如果检验 pH 值在参考 pH 值的 10% 范围内,工程师会将这两种抗酸药视为等价。
工程师执行 2x2 交叉设计的等价检验,以确定检验 pH 值与参考 pH 值是否等价。差值的置信区间不完全包含在置信区间 (–0.425, 0.425) 内。因此,工程师不能声明这两种抗酸药等价。为了改进下一个研究的设计,工程师通过计算功效和样本大小来评估需要多大的样本才能使检验功效达到 90% (0.9)。根据前面的样本,工程师估计总体的对象内标准差为 0.088。
- 选择。
- 从相关假设中,选择检验均值 - 参考均值 (差值)。
- 从您要确定什么? (备择假设)中,选择下限 < 检验均值 - 参考均值 < 上限。
- 在下限中,输入 -0.425。在上限中,输入 0.425。
- 在差值(在限值内)中,输入 0 0.1 0.2 0.3 0.4。
- 在功效值中,输入 0.9。
- 在主题组内标准差中,输入 0.088。
- 单击确定。
解释结果
如果差值为 0.1,则工程师仅需要每个序列中包括 2 名参与者即可达到至少 0.9 的功效(实际功效大约为 0.93)。
当差值接近等价上限 (0.425) 时,工程师需要使用更多的观测值才能达到同样的功效。例如,对于差值 0.4,工程师需要每个序列至少包括 107 名参与者才能达到功效 0.9。
对于任何样本数量,当差值接近等价下限或等价上限时,检验的功效会降低并接近 α(alpha,即在不等价时声明等价的风险)。
方法
| 差值的功效: | 检验均值 - 参考均值 |
|---|---|
| 原假设: | 差值 ≤ -0.425 或差值 ≥ 0.425 |
| 备择假设: | -0.425 < 差值 < 0.425 |
| α 水平: | 0.05 |
结果
| 差值 | 样本数量 | 目标功效 | 实际功效 |
|---|---|---|---|
| 0.0 | 2 | 0.9 | 0.978589 |
| 0.1 | 2 | 0.9 | 0.931544 |
| 0.2 | 3 | 0.9 | 0.972795 |
| 0.3 | 6 | 0.9 | 0.943646 |
| 0.4 | 107 | 0.9 | 0.900500 |