请选择您所选的方法或公式。
计算检验均值 – 参考均值(差值)的功效
功效
假设 tα,v 是自由度为 v 的 t 分布的 α(单侧)临界值上限。双侧备择假设下限 < 检验均值 - 参考均值 < 上限的功效计算公式如下:
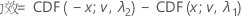
对于备择假设检验均值 > 参考均值或检验均值 - 参考均值 > 下限,功效计算公式如下:

对于备择假设检验均值 < 参考均值或检验均值 - 参考均值 < 上限,功效计算公式如下:

其中 CDF(x; v, λ) 是针对具有非中心参数 λ 和自由度 v 的非中心 t 分布,在 x 处求值的累积分布函数。
自由度
自由度 v 的计算公式如下:

对于功效计算,假定这两个组的 n 相等。
非中心参数
对应于等价下限的非中心参数用 λ1 表示,其计算公式如下:
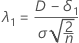
对于备择假设检验均值 > 参考均值,δ1 = 0。
对应于等价上限的非中心参数用 λ2 表示,其计算公式如下:
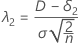
对于备择假设检验均值 < 参考均值,δ2 = 0。
表示法
| 项 | 说明 |
|---|---|
| α | 检验的显著性水平 |
| D | 检验总体的均值减去参考总体的均值 |
| δ1 | 等价下限 |
| δ2 | 等价上限 |
| n | 样本数量(对于功效计算,假定这两个组的 n 相等。) |
| σ | 总体的标准差(对于功效计算,假设这两个总体的 σ 相等。) |
计算检验均值/参考均值(比值,用对数变换表示)的功效
本主题描述当在相关假设中选择检验均值 / 参考均值 (比值,通过对数变换)时如何计算功效。
功效
假设 tα,n 是自由度为 v 的 t 分布的 α(单侧)临界值上限。双侧备择假设下限 < 检验均值 / 参考均值 < 上限的功效计算公式如下:

对于备择假设检验均值 / 参考均值 > 下限,功效计算公式如下:

对于备择假设检验均值 / 参考均值 < 上限,功效计算公式如下:

其中 CDF(x; v, λ) 是针对具有非中心参数 λ 和自由度 v 的非中心 t 分布,在 x 处求值的累积分布函数。
自由度
自由度 v 的计算公式如下:

对于功效计算,假定这两个组的 n 相等。
非中心参数
对应于等价下限的非中心参数用 λ1 表示,其计算公式如下:
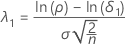
对应于等价上限的非中心参数用 λ2 表示,其计算公式如下:
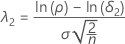
西格玛
标准差 σ 是使用变异系数 CV 计算的,如下所示:

表示法
| 项 | 说明 |
|---|---|
| α | 检验的显著性水平 |
| ρ | 检验总体均值与参考总体均值之间的比值 |
| δ1 | 等价下限 |
| δ2 | 等价上限 |
| n | 样本数量(对于功效计算,假定这两个组的 n 相等。) |
