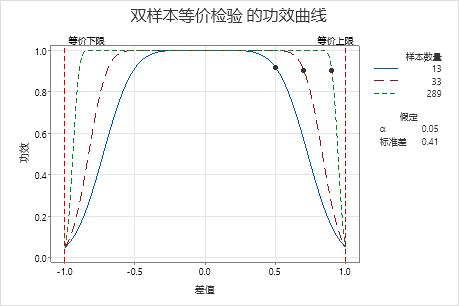
某质量分析员想要确定一般品牌的止痛药中有效成分的平均含量是否在名牌止痛药中有效成分的平均含量的 1 mg 范围内。在为双样本等价检验收集数据之前,分析员通过计算功效和样本数量来确定样本必须多大才能使功效达到 90% (0.9)。根据前面的样本,分析员估计得出总体标准差为 0.41。
- 选择。
- 从相关假设中,选择检验均值 - 参考均值 (差值)。
- 从您要确定什么? (备择假设)中,选择下限 < 检验均值 - 参考均值 < 上限。
- 在下限中,输入 -1。在上限中,输入 1。
- 在差值(在限值内)中,输入 0.5 0.7 0.9。
- 在功效值中,输入 0.9。
- 在标准差中,输入 0.41。
- 单击确定。
解释结果
如果差值为 0.5,则分析员要求每组中有 13 个观测值才能达到至少 0.9 的功效。如果分析员使用样本数量 13,则检验的功效大约为 0.92。
当差值靠近等价下限 (–1) 或等价上限 (1) 时,分析员需要使用较大的样本数量才能达到相同的功效。例如,对于差值 0.9,分析员需要使用每组中至少包含 289 个观测值的样本数量,才能达到功效 0.9。
对于任何样本数量,当差值接近等价下限或等价上限时,检验的功效会降低并接近 α(alpha,即在不等价时声明等价的风险)。
方法
| 差值的功效: | 检验均值 - 参考均值 |
|---|---|
| 原假设: | 差值 ≤ -1 或差值 ≥ 1 |
| 备择假设: | -1 < 差值 < 1 |
| α 水平: | 0.05 |
| 假定的标准差: | 0.41 |
结果
| 差值 | 样本数量 | 目标功效 | 实际功效 |
|---|---|---|---|
| 0.5 | 13 | 0.9 | 0.915407 |
| 0.7 | 33 | 0.9 | 0.902461 |
| 0.9 | 289 | 0.9 | 0.900360 |