单样本等价检验的功效和样本数量 的方法和公式

功效

假设 t_α,v 是自由度为 v 的 t 分布的 α（单侧）临界值上限。双侧备择假设下限 < 检验均值 - 目标值 < 上限的功效计算公式如下：

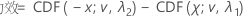
对于备择假设检验均值 > 目标值或检验均值 - 目标值 > 下限，功效计算公式如下：

对于备择假设检验均值 < 目标值或检验均值 - 目标值 < 上限，功效计算公式如下：

其中 CDF(x; v, λ) 是针对具有非中心参数 λ 和自由度 v 的非中心 t 分布，在 x 处求值的累积分布函数。

自由度

自由度 v 的计算公式如下：

非中心参数

对应于等价下限的非中心参数用 λ₁ 表示，其计算公式如下：

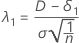
对于备择假设检验均值 > 目标值，δ₁ = 0。

对应于等价上限的非中心参数用 λ₂ 表示，其计算公式如下：

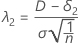
对于备择假设检验均值 < 目标值，δ₁ = 0。

表示法

项	说明
α	检验的显著性水平
D	检验总体的均值减去目标值
δ1	等价下限
δ2	等价上限
n	样本数量
σ	总体的标准差

如果您提供了功效和差值，Minitab 将计算样本数量。Minitab 将使用适当的功效公式和迭代算法来确定其功效大于或等于指定值的最小样本数量 n。n 的实际功效有可能大于指定的功效。这是由于 n 必须是离散的整数值，任何值 n 都不可能生成与指定的功效值完全相同的值。

如果您提供了功效和样本数量的值，Minitab 将计算差值。Minitab 使用适当的功效公式和迭代算法来确定其功效大于或等于指定值的最大和/或最小差值。