检验统计量
- Minitab 对两个组合样本排秩。Minitab 为最小的观测值分配秩 1，为第二小的观测值分配秩 2，以此类推。
- 如果将两个或更多观测值相结合，Minitab 将为这两个观测值分配平均秩。
- Minitab 求第一个样本的秩的和。
对已结合的值排秩
- 按升序对观测值进行排序。
- 为每个观测值分配秩，就好像没有结一样。
- 对于已结合的集，求相应秩的平均数并将该值作为新秩分配给此集内的每个已结合的值。
示例
一个样本有 9 个观测值：2.4、5.3、2.4、4.0、1.2、3.6、4.0、4.3 和 4.0。
| 观测值 | 秩
（假定无结） |
秩 | |
|---|---|---|---|
| 1.2 | 1 | 1 | |
| 已结合 | 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 | |
| 3.6 | 4 | 4 | |
| 已结合 | 4.0 | 5 | 6 |
| 4.0 | 6 | 6 | |
| 4.0 | 7 | 6 | |
| 4.3 | 8 | 8 | |
| 5.3 | 9 | 9 |
- 结集的数量为 2。
- 位于第一个集中的已结合的值的数量为 2。
- 位于第二个集中的已结合的值的数量为 3。
P 值
公式
Mann-Whitney 检验使用正态近似方法来确定检验的 p 值。
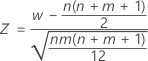的分布与均值为 0 且标准差为 1 的正态分布 N(0,1) 近似。
| 备择假设 | P 值 |
|---|---|
| H1：η1 > η2 |  |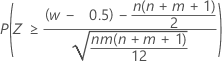
| H1：η1 < η2 |  |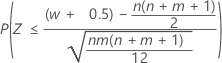
| H1：η1 ≠ η2 |  |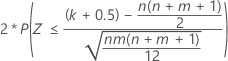
调整后的 p 值通常比未调整的 p 值更准确。但是，未调整的 p 值是更保守的估计值，其原因是对于特定的样本对，未调整的 p 值始终大于调整后的 p 值。
表示法
| 项 | 说明 |
|---|---|
| W | Mann-Whitney 检验统计量 |
| n | 样本 1 的数量 |
| m | 样本 2 的数量 |
| η1 | 样本 1 的中位数 |
| η2 | 样本 2 的中位数 |
| k |  |
| ii | 1, 2, …, I |
| I | 结集的数量 |
| ti | 第 i 组结中已结合的值的数量 |
点估计
以下文章中介绍了 Minitab 用来计算 η1 – η2 的点估计值的近似算法：J.W. McKean 和 T.A. Ryan, Jr. (1977)。“An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem”（一种基于双样本位置问题中的秩获得置信区间和点估计的算法），《Transactions on Mathematical Software》（数学软件汇刊），第 183–185 页。
置信区间
η1 – η2 的置信区间定义为 η1 – η2 的值范围，在此范围内不否定原假设。
以下文章中介绍了 Minitab 用来计算置信区间的方法：J.W. McKean 和 T.A. Ryan, Jr. (1977)。“An Algorithm for Obtaining Confidence Intervals and Point Estimates Based on Ranks in the Two Sample Location Problem”（一种基于双样本位置问题中的秩获得置信区间和点估计的算法），《Transactions on Mathematical Software》（数学软件汇刊），第 183-185 页。
