请选择您所选的方法或公式。
平均秩
Minitab 按如下方式计算平均秩:
- 对组合样本排秩,为最小的观测值分配秩 1,为第二小的观测值分配秩 2,以此类推。
- 如果将两个或更多观测值相结合,Minitab 将为这两个观测值分配平均秩。
- 计算每个样本的秩的平均数。
Minitab 将每个组的值显示在输出中的“平均秩”下。
Z 值
公式
Minitab 按如下方式计算每个组的 z 值:
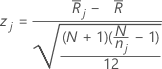
表示法
| 项 | 说明 |
|---|---|
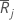 | 组 j 的平均秩 |
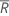 | 所有观测值的平均秩 |
| N | 观测值个数 |
| nj | 第 j 组的观测值个数 |
对已结合的值排秩
当两个或多个观测值相等时,会出现已结合的值。如果数据中有已结合的值,Minitab 会按如下方式对数据排秩:
- 按升序对观测值进行排序。
- 为每个观测值分配秩,就好像没有结一样。
- 对于已结合的集,求相应秩的平均数并将该值作为新秩分配给此集内的每个已结合的值。
示例
一个样本有 9 个观测值:2.4、5.3、2.4、4.0、1.2、3.6、4.0、4.3 和 4.0
| 观测值 | 秩(假定无结) | 秩 |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
还可以使用以下信息来计算检验统计量:
- 结集的数量 = 2
- 位于第一个集中的已结合的值的数量 = 2
- 位于第二个集中的已结合的值的数量 = 3
H
公式

在原假设下,自由度为 k – 1 的卡方分布与 H 的分布近似。当所有组的观测值个数都不少于 5 时,这种近似的准确度比较合理。H 值越大,证明原假设(一些中位数之间的差异在统计意义上显著)成立的证据越充分。
某些作者(例如,Lehmann (1975)1)建议在数据有结时调整 H。当数据有结时,Minitab 会显示 H(adj)。
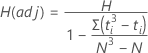
在原假设下,自由度为 k – 1 的卡方分布与 H 和 H(adj) 的分布近似。
P 值 = 1 – CDF (χ2H, df)
P 值 = 1 – CDF (χ2H(adj), df)
对于小样本,Minitab 建议使用精确表。有关更多详细信息,请参见 Hollander 和 Wolfe (1973)2。
表示法
| 项 | 说明 |
|---|---|
| nj | 组 j 中的观测值个数 |
| N | 总样本数量 |
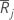 | 组 j 中秩的平均值 |
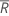 | 所有秩的平均值 |
| ti | 第 i 组结中已结合的值的数量 |
1 E.L. Lehmann (1975)。《Nonparametrics: Statistical Methods Based on Ranks》(非参数统计:基于秩的统计方法),Holden-Day
2 M. Hollander 和 D.A. Wolfe (1973)。《Nonparametric Statistical Methods》(非参数统计方法),John Wiley & Sons, Inc.
