S
检验统计量具有近似卡方 ( χ2) 分布,与该分布相关的自由度为 (k – 1)。如果一个或多个区组中的数据有结,Minitab 将使用平均秩并打印已针对结进行校正的检验统计量。有关此方法的详细信息,请参见 M. Hollander 和 D.A. Wolfe (1973)1。
公式
要计算卡方检验统计量,Minitab 对每个区组中的数据单独排秩并求每个处理的秩的和。
如果数据中没有结,则公式为:
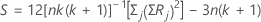
如果数据中有结,则公式为:

其中,C 是校正因子,它等于:
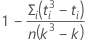
表示法
| 项 | 说明 |
|---|---|
| j | 1, 2, ..., k |
| k | 处理条件的数量 |
| n | 区组数 |
| Rj | 第 j 个处理的秩的和 |
| ii | 1, 2, ..., m |
| m | 结集的数量 |
| ti | 第 i 组结中已结合的分值的数量 |
- M. Hollander 和 D.A. Wolfe (1973)。Nonparametric Statistical Methods(非参数统计方法),John Wiley & Sons, Inc.
总中位数
要了解如何计算处理效应、区组中位数和总中位数,请考虑以下数据。
| 区组 | ||||
| 处理 | 1 | 2 | 3 | 4 |
| 1 | 0.15 | 0.26 | 0.23 | 0.99 |
| 2 | 0.55 | 0.26 | −0.22 | 0.99 |
| 3 | 0.55 | 0.66 | 0.77 | 0.99 |
要计算处理效应(Doksum 方法1),请首先查找处理对之间的中位数差值。处理 1 的配对差减去处理 2 的配对差为:0.15 - 0.55 = −0.4,0.26 – 0.26 = 0,0.23 – (−0.22) = 0.45,0.99 – 0.99 = 0。这些差值的中位数为 0。针对另外两对执行此计算将得到 −0.4(处理 1 减去处理 3)和 −0.2(处理 2 减去处理 3)。
每个处理的效应是该处理与所有其他处理(包括该处理本身)的中位数差值的平均值。对于本例中的数据,效应(2) = [中位数 (2 – 1) + 中位数 (2 – 2) + 中位数 (2 – 3)]/3 = (0.00 + 0.00 – 0.20)/3 = −0.0667。同样,效应(1) = −0.1333,效应(3) = 0.20。
要计算调整后的区组中位数,请通过将观测值减去相应的处理效应来调整每个观测值。调整后的区组中位数只是这些调整后数据(在每个区组内计算)的中位数。总中位数是已调整的区组中位数的中位数。每个处理水平的中位数估计值等于处理效应与总中位数的和。
- M. Hollander 和 D.A. Wolfe (1973)。Nonparametric Statistical Methods(非参数统计方法),John Wiley & Sons, Inc.,第 158 – 161 页。
对已结合的值排秩
- 按升序对观测值进行排序。
- 为每个观测值分配秩,就好像没有结一样。
- 对于已结合的集,求相应秩的平均数并将该值作为新秩分配给此集内的每个已结合的值。
示例
一个样本有 9 个观测值:2.4、5.3、2.4、4.0、1.2、3.6、4.0、4.3 和 4.0
| 观测值 | 秩(假定无结) | 秩 |
|---|---|---|
| 1.2 | 1 | 1 |
| 2.4 | 2 | 2.5 |
| 2.4 | 3 | 2.5 |
| 3.6 | 4 | 4 |
| 4.0 | 5 | 6 |
| 4.0 | 6 | 6 |
| 4.0 | 7 | 6 |
| 4.3 | 8 | 8 |
| 5.3 | 9 | 9 |
- 结集的数量 = 2
- 位于第一个集中的已结合的值的数量 = 2
- 位于第二个集中的已结合的值的数量 = 3
