请选择您所选的方法或公式。
配对平均数
配对平均数（也称为 Walsh 平均数）是数据集内每个可能的值对的均值，包括每个值与其本身组成的值对。
公式
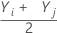= i ≤ j 的所有配对平均数。
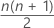= 配对平均数的总数
表示法
| 项 | 说明 |
|---|---|
| Yi | 数据集内的第 i 个值 |
| Yj | 数据集内的第 j 个值 |
| n | 样本数量 |
中位数估计值
假设 W( 1 )< W( 2 )< ... < W( M ) 表示配对平均数（又称为 Walsh 平均数）的排序值，其中 M = n(n+1)/2。如果 M 是奇数，则中位数估计值是中间的值。如果 M 是偶数，则中位数估计值是两个中间值的平均数。Minitab 使用基于 Johnson 和 Mizoguchi (1978)1 的算法获得总体中位数的点估计值。
- D.B. Johnson 和 T. Mizoguchi (1978)。“Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm”（在 X + Y 和 X1 + X2 + ... + Xm 中选择第 K 个元素），《SIAM Journal of Computing》（SIAM 计算杂志）第 7 期，第 147-153 页。
Wilcoxon 统计量
Wilcoxon 统计量是超过假设中位数的配对平均数（又称为 Walsh 平均数）的数量与 1/2 的等于假设中位数的配对平均数的数量之和。Wilcoxon 统计量用 W 表示。Minitab 使用基于 Johnson 和 Miizoguchi (1978)1 的算法获取检验统计量。
- D.B. Johnson 和 T. Mizoguchi (1978)。“Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm”（在 X + Y 和 X1 + X2 + ... + Xm 中选择第 K 个元素），《SIAM Journal of Computing》（SIAM 计算杂志）第 7 期，第 147-153 页。
P 值
Wilcoxon 检验统计量 W 是与超过假设中位数的观测值个数相关联的秩的和。Minitab 按照 Johnson 和 Mizoguchi1 中的说明，使用配对 (Walsh) 平均数来计算检验统计量。
- 针对每个等于假设中位数的观测值，观测值个数 N 会按一递减。所生成的样本数量为 n。
- 排除等于假设中位数的观测值。对于 i ≤ j 个观测值，计算 n(n + 1) / 2 个配对 Walsh 平均数 (Yi + Yj) / 2。
对于大样本，W 的分布近似正态。具体来说：
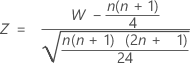的分布与均值为 0 且标准差为 1 的正态分布 N(0,1) 近似。
三个备择假设的正态近似 p 值使用连续校正值 0.5。
| 备择假设 | P 值 |
|---|---|
| H1：中位数 > 假设中位数 |  |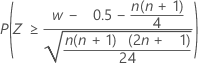
| H1：中位数 < 假设中位数 |  |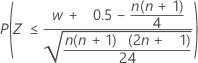
| H1：中位数 ≠ 假设中位数 |  |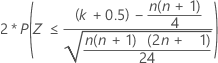
表示法
| 项 | 说明 |
|---|---|
| n | 在省略了等于假设中位数值的任何观测值之后，观测到的数据点个数 |
| W | Wilcoxon 检验统计量 |
| w | 超过假设中位数的 Walsh 平均数的数量与 1/2 的等于假设中位数的 Walsh 平均数的数量之和。 |
| k |  |
- D.B. Johnson 和 T. Mizoguchi (1978)。“Selecting the Kth Element in X + Y and X1 + X2 + ... + Xm”（在 X + Y 和 X1 + X2 + ... + Xm 中选择第 K 个元素），《SIAM Journal of Computing》（SIAM 计算杂志）第 7 期，第 147-153 页。
置信区间
置信区间是一组值 (d)，对于这些值，不否定“H0：中位数 = d”检验，支持“H1：中位数 ≠ d”检验，使用的置信水平为（α = 1 - (置信百分比) / 100）。单样本 Wilcoxon 检验并不总是能够实现指定的置信水平，这是因为 Wilcoxon 统计量是离散的。因此，Minitab 结合使用正态近似和连续校正来计算可实现且最接近的置信水平。
