下列方法和公式用于对检验均值和参考均值之间的比值进行检验。
比值
比值 ρ 等于检验均值 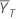 除以参考均值
除以参考均值 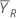 ,如下所示:
,如下所示:
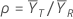


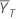 除以参考均值
除以参考均值 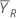 ,如下所示:
,如下所示:
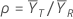


合并方差
参考周期的合并方差 S2RR 按如下公式计算:
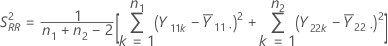
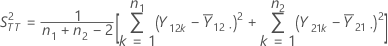
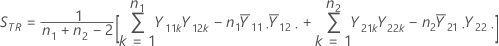
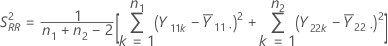
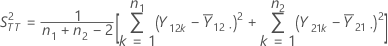
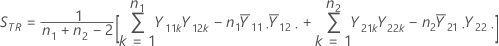
表示法
| 项 | 说明 |
|---|---|
| Yijk | 序列 i 中参与者 k 在周期 j 过程中的响应(有关更多信息,请转到2x2 交叉设计的等价检验 中使用的常见概念的方法和公式。) |
| ni | 序列 i 中参与者的数量 |
等价置信区间
100(1-α)% CI
如果未满足下面两个条件中的任意一个条件,Minitab 将无法计算置信区间 (CI):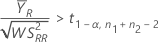

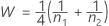
CI = [min(C, ρL), max(C, ρU)]
其中:
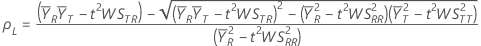
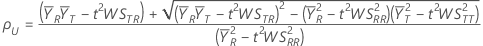
100(1-2α)% CI
如果您选择与使用 100(1 – 2 α)% CI 相对应的选项,则将按如下公式计算 CI:CI = [ρL, ρU]
单边区间
对于假设检验均值 / 参考均值 > 下限,100(1 – α)% 下限等于 ρL。
对于假设检验均值 / 参考均值 < 上限,100(1 – α)% 上限等于 ρU。
表示法
| 项 | 说明 |
|---|---|
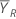 | 参考期间的均值(有关详细信息,请参见有关比值的部分) |
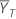 | 检验期间的均值(有关详细信息,请参见有关比值的部分) |
| ni | 序列 i 中参与者的数量 |
| v | 自由度 |
| α | 检验的显著性水平 (alpha) |
| t1-α,v | 自由度为 v 的 t 分布的 1 – α 上临界值 |
T 值
假定 t1 是如下假设的 t 值: ,假定 t2 是如下假设的 t 值:
,假定 t2 是如下假设的 t 值: ,其中
,其中  是总体的检验均值与参考均值之间的比值。可按如下公式计算 t 值:
是总体的检验均值与参考均值之间的比值。可按如下公式计算 t 值:
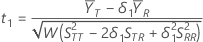
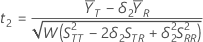
 ,假定 t2 是如下假设的 t 值:
,假定 t2 是如下假设的 t 值: ,其中
,其中  是总体的检验均值与参考均值之间的比值。可按如下公式计算 t 值:
是总体的检验均值与参考均值之间的比值。可按如下公式计算 t 值:
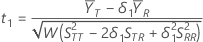
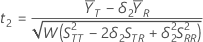
表示法
| 项 | 说明 |
|---|---|
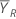 | 参考期间的均值(有关详细信息,请参见有关比值的部分) |
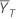 | 检验期间的均值(有关详细信息,请参见有关比值的部分) |
| δ1 | 等价下限 |
| δ2 | 等价上限 |
P 值
每个原假设的概率 PH0 按如下公式进行计算:
如果  ,那么:
,那么:
| H0 | P 值 |
|---|---|
 |
 |
 |
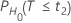 |
表示法
| 项 | 说明 |
|---|---|
| Λ | 检验总体的均值与参考总体的均值之间的未知比值 |
| δ1 | 等价下限 |
| δ2 | 等价上限 |
| v | 自由度 |
| T | 自由度为 v 的 t 分布 |
| t1 | 如下假设的 t 值: |
| t2 | 如下假设的 t 值: |
注意
有关如何计算 t 值的信息,请参见与 t 值有关的部分。
