某家宠物食品公司的食品科学工程师对其畅销的猫食的低成本新配方进行检验。该工程师想要确保低成本配方的蛋白质含量与原始猫食的蛋白质含量相同。该工程师测量了这两种猫食配方的样本(100 克)中的蛋白质含量,以检验这些含量是否相等(差异在 ±0.5 克范围内)。
该工程师执行了双样本等价检验,以确定这两种配方的蛋白质均值差异是否在 ±0.5 克范围内。该工程师不知道这两种配方的蛋白质含量的变异是否相等。
- 打开样本数据,猫粮蛋白质含量.MWX。
- 选择。
- 从下拉列表中,选择样本在不同列中。
- 在检验样本中,输入折扣。
- 在参考样本中,输入原始。
- 从相关假设中,选择检验均值 - 参考均值。
- 从您要确定什么? (备择假设)中,选择下限 < 检验均值 - 参考均值 < 上限。
- 在下限中,输入 –0.5。
- 在上限中,输入 0.5。
- 单击确定。
解释结果
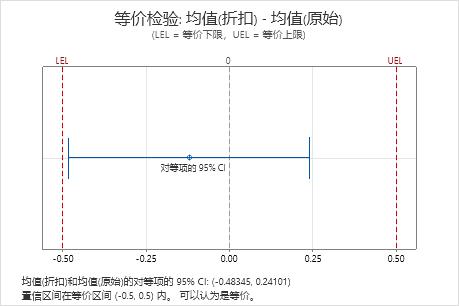
由于置信区间完全包含在等价区间内,因此工程师得出了两个猫粮配方的蛋白质含量等价的结论。
方法
检验均值 = 折扣 的均值
参考均值 = 原始 的均值
未针对此分析假定相等方差。
参考均值 = 原始 的均值
未针对此分析假定相等方差。
描述性统计量
| 变量 | N | 均值 | 标准差 | 均值标准误 |
|---|---|---|---|---|
| 折扣 | 10 | 33.971 | 0.58064 | 0.18361 |
| 原始 | 9 | 34.092 | 0.26138 | 0.087127 |
差值: 均值(折扣) - 均值(原始)
| 差值 | SE | 对等项的 95% CI | 等价区间 |
|---|---|---|---|
| -0.12122 | 0.20324 | (-0.483449, 0.241005) | (-0.5, 0.5) |
检验
| 原假设: | 差值 ≤ -0.5 或差值 ≥ 0.5 |
|---|---|
| 备择假设: | -0.5 < 差值 < 0.5 |
| α 水平: | 0.05 |
| 原假设 | 自由度 | T 值 | P 值 |
|---|---|---|---|
| 差值 ≤ -0.5 | 12 | 1.8637 | 0.044 |
| 差值 ≥ 0.5 | 12 | -3.0566 | 0.005 |