自由度 (DF) 是数据提供的信息量,您可以使用这些信息来估计未知总体参数的值并计算这些估计值的变异性。自由度值由样本中的观测值个数和模型中的参数个数确定。
增加样本数量可提供有关总体的更多信息,从而增加数据中的自由度。向模型中添加参数(例如,通过增加回归等式中的项数)会“占用”数据中的信息,并降低可用来估计参数估计值的变异性的自由度。
自由度还用于确定特定分布的特征。许多分布系列(如 t 分布、F 分布和卡方分布)都使用自由度来指定适用于不同样本数量和不同模型参数个数的特定 t 分布、F 分布或卡方分布。例如,下图描述具有不同自由度的卡方分布之间的差异。
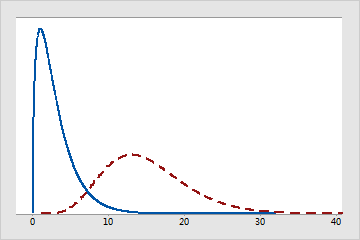
具有不同自由度的卡方分布
实线分布的自由度为 3。虚线分布的自由度为 15。
示例
例如,单样本 t 检验仅估计一个参数:总体均值。样本数量 n 构成 n 段用于估计总体均值及其变异性的信息。一个自由度用于估计均值,其余的 n-1 个自由度用于估计变异性。因此,单样本 t 检验使用具有 n-1 个自由度的 t 分布。
相反,多重线性回归必须为您选择包括在模型中的每个项估计一个参数,每个项都占用一个自由度。因此,在多重线性回归模型中包括多余项会降低用来估计参数变异性的自由度,并且会降低模型的可靠性。
