什么是参数、参数估计值和抽样分布？

当您需要确定特定某总体特征（例如均值）的信息时，通常从总体中取一些随机样本，因为对总体进行度量是不可行的。通过使用该样本，您可以计算对应样本的特征，其用于概括关于未知总体特征的信息。所需的总体特征称为参数，相应样本特征为样本统计量或参数估计值。由于统计量是对从样本获取的参数的信息的摘要，因此统计量值取决于从总体中取的特定样本。其值随机地从一个随机样本更换到下一个随机样本，因此统计量是一个随机量（变量）。此随机变量的概率分布称为取样分布。（样本）统计量的采样分布很重要，因为它使我们能够基于随机抽样得出关于相应总体参数的结论。

例如，当我们从一个正态分布总体中取随机样本时，样本均值就是一个统计量。基于样本的样本均值是对总体均值的估计。如果从该同一正态总体中取不同的样本，该估计值将随机变化。用于描述这些变化的概率分布是样本均值的抽样分布。统计量的采样分布指定了统计量的所有可能值，以及统计量值的极差的变化频率。如果总体为正态，则样本均值的采样分布也为正态。

以下各节提供有关参数、参数估计值和采样分布的详细信息。

关于参数

参数是整个总体的描述性度量，它可用作概率分布函数 (PDF) 的输入以生成分布曲线。参数通常用希腊字母表示，以与样本统计量区别开来。例如，总体均值由希腊字母 mu (μ) 表示，总体标准差由希腊字母 sigma (σ) 表示。参数是固定常量，也就是说，它们不会像变量一样变化。不过，它们的值通常是未知的，因为对整个总体进行度量是不可行的。

每个分布完全由若干个特定参数来定义，参数的个数通常为一到三个。下表提供了三种分布所需参数的示例。参数值决定了分布图上的曲线的位置和形状，参数值的每个唯一组合可产生唯一的分布曲线。

分布	参数 1	参数 2	参数 3
卡方	自由度
正态	均值	标准差
3 参数 Gamma	形状	尺度	阈值

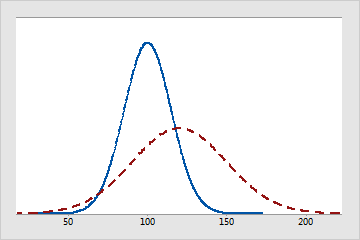
例如，正态分布由两个参数定义，即均值和标准差。如果指定了这两个参数，可以精确确定整个分布。

实线表示一个正态分布（其均值为 100，标准差为 15）。虚线也是一个正态分布，但它的均值为 120，标准差为 30。

关于参数估计值（也称为样本统计量）

参数是对整个总体的描述性度量。不过，它们的值通常是未知的，因为对整个总体进行度量是不可行的。因此，您可以从总体取一个随机样本以获得参数估计值。统计分析的一个目标是获得总体参数的估计值，以及与这些估计关联的误差量。这些估计值也称为样本统计量。

存在若干种类型的参数估计值：

点估计值是参数的单一且最可能值。例如，总体均值（参数）的点估计值是样本均值（参数估计值）。
置信区间是可能包含总体参数的值范围。

对于参数估计值的示例，假设您为一家火花塞制造商工作，该公司正在研究火花塞间隙存在的问题。要检验其所生产的每个火花塞，成本太高。于是，您随机抽取了 100 个火花塞，并以毫米为单位度量间隙。样本均值为 9.2。这是总体均值 (μ) 的点估计值。您还为 μ 创建了一个 95% 置信区间，该区间为 (8.8, 9.6)。您也可以为 μ（8.8，9.6）创建一个 95% 的置信区间。

关于采样分布

采样分布是给定统计量（例如均值）的概率分布。为了说明抽样分布，让我们来看一个简单示例，其中完整总体是已知的。例如，下表显示了整个总体（6 个南瓜）的重量。这些南瓜的重量只能是下表中列出的重量值之一。

南瓜	1	2	3	4	5	6
重量	19	14	15	12	16	17

虽然整个总体是已知的，但是为了便于说明，我们从总体中取包含 3 个南瓜的所有可能随机样本（20 个随机样本）。然后，计算各样本的均值。样本均值的取样分布由每个可能随机样本（包含 3 个南瓜）的所有样本均值描述，其显示在下表中。

样本	重量	平均重量	概率
2, 3, 4	14, 15, 12	13.7	1/20
2, 4, 5	14, 12, 16	14	1/20
2, 4, 6	14, 12, 17	14.3	2/20
3, 4, 5	15, 12, 16	14.3	2/20
3, 4, 6	15, 12, 17	14.7	1/20
1, 2, 4	19, 14, 12	15	3/20
2, 3, 5	14, 15, 16
4, 5, 6	12, 16, 17
2, 3, 6	14, 15, 17	15.3	2/20
1, 3, 4	19, 15, 12	15.3	2/20
1, 4, 5	19, 12, 16	15.7	2/20
2, 5, 6	14, 16, 17	15.7	2/20
1, 2, 3	19, 14, 15	16	3/20
3, 5, 6	15, 16, 17
1, 4, 6	19, 12, 17
1, 2, 5	19, 14, 16	16.3	1/20
1, 2, 6	19, 14, 17	16.7	2/20
1, 3, 5	19, 15, 16	16.7	2/20
1, 3, 6	19, 15, 17	17	1/20
1, 5, 6	19, 16, 17	17.3	1/20

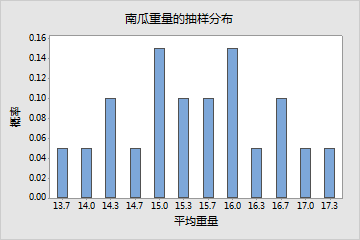
此图显示了平均重量值的采样分布。此分布围绕 15.5（这也是总体均值的真值）。其样本均值较接近 15.5 的随机样本的发生概率，比其样本均值较远离 15.5 的随机样本的发生概率更高。

在实际中，生成以上所示的采样分布表是不可行的。即使在最佳情况下（即知道样本的父级总体），可能仍无法确定所需样本统计量的精确采样分布。但是，在某些情况下，可能能够大致地确定样本量统计的采样分布。例如，如果从正态总体中取样，则样本平均值具有完全的正态分布。

但是，如果从一个非正态分布中抽样，则可能无法确定样本均值的准确分布。但是，由于中心极限定理，样本均值近似地呈正态分布，前提是您的样本足够大。然后，如果总体未知并且样本足够大，则您也许能够做出判断（例如，85% 地判断样本均值在一定数量的总体均值的标准差之内）。