中心极限定理是概率和统计量的基本定理。该定理描述具备有限方差的总体的随机样本的均值分布。当样本数量足够大时,均值的分布呈近似正态分布。无论总体的分布形状如何,中心极限定理均适用。许多常见的统计过程都要求数据呈近似正态分布。中心极限定理允许您将这些有用的过程应用到与正态分布相差很大的总体。样本数量必须为多大取决于原始分布的形状。如果总体的分布是对称的,则样本数量 5 可生成不错的近似值。如果总体的分布极其不对称,则有必要使用更大的样本数量。例如,如果样本数量大于 50,则均值的分布可能呈近似正态分布。下面的几幅图显示了分布对所需样本数量的影响。
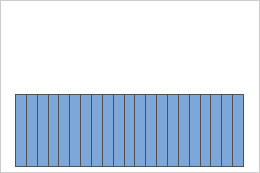
均匀分布
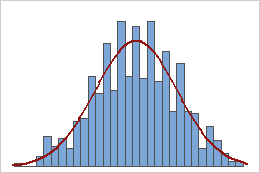
样本均值
均匀总体的样本
服从均匀分布的总体是对称的,但其分布与正态分布相差很大,如第一个直方图所示。但是,根据中心极限定理,此总体的 1000 个数量为 5 的样本的样本均值的分布则近似为正态,如第二个直方图所示。此样本均值直方图包括一个叠加的正态曲线,揭示了其正态性。
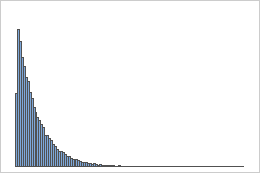
指数分布
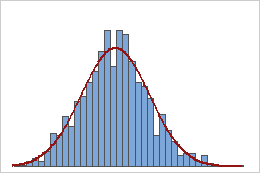
样本均值
指数总体的样本
服从指数分布的总体是不对称的,并且是非正态的,如第一个直方图所示。但是,根据中心极限定理,此总体的 1000 个数量为 50 的样本的样本均值的分布则近似为正态,如第二个直方图所示。此样本均值直方图包含一个叠加的正态曲线,揭示了其正态性。
