什么是相关?
相关系数可度量两个变量倾向于同时变化的程度。该系数同时描述了关系的强度和方向。Minitab 提供两个不同的相关分析:
- Pearson 积矩相关
-
Pearson 相关评估两个连续变量之间的线性关系。当一个变量中的变化与另一个变量中的成比例变化相关时,这两个变量具有线性关系。
例如,您可能使用 Pearson 相关来评估您生产设施温度的升高是否与巧克力涂层的厚度减少有关。
- Spearman 秩次相关
-
Spearman 相关评估两个连续或顺序变量之间的单调关系。在单调关系中,变量倾向于同时变化,但不一定以恒定的速率变化。Spearman 相关系数基于每个变量的秩值(而非原始数据)。
Spearman 相关通常用于评估与顺序变量相关的关系。例如,您可能会使用 Spearman 相关来评估员工完成检验练习的顺序是否与他们工作的月数相关。
最好始终用散点图来检查变量之间的关系。相关系数仅度量线性 (Pearson) 或单调 (Spearman) 关系。也有可能存在其他关系。
对 Pearson 和 Spearman 系数进行比较
Pearson 和 Spearman 相关系数的值介于 −1 和 +1 之间。当两个变量的上升量相同时,Pearson 相关系数为 +1。该关系会构成一条完美的直线。在本例中,Spearman 相关系数也是 +1。


Pearson = +1,Spearman = +1
如果关系是一个变量上升,其他变量也上升,但上升量不一致,则 Pearson 相关系数为小于 +1 的正数。在本例中,Spearman 系数仍等于 +1。

Pearson = +0.851,Spearman = +1
当存在随机关系或者不存在关系时,这两个相关系数都接近零。


Pearson = −0.093,Spearman = −0.093
如果关系对应的是一条完美的下降关系直线,则这两个相关系数都为 −1。


Pearson = −1,Spearman = −1
如果关系是一个变量下降,其他变量上升,但变化程度不一致,则 Pearson 相关系数为大于 −1 的负数。在本例中,Spearman 系数将仍等于 −1。


Pearson = −0.799,Spearman = −1
相关值 −1 或 1 表明存在完全线性关系,例如,圆的半径和周长之间的关系。但是,在量化分析中,相关值的实际值小于完美关系的值。确定两个变量相关通常表示需要进行回归分析,从而尝试更详细地描述这种类型的关系。
其他非线性关系
Pearson 相关系数只度量线性关系。Spearman 相关系数只度量单调关系。因此,即使相关系数为 0,也可能存在有意义的关系。检查散点图可确定关系的形式。
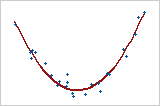

系数 0
此图形显示非常强的关系。Pearson 系数和 Spearman 系数都近似 0。
