临界值是在原假设下,检验统计量在分布图上的点,这些点定义一组要求否定原假设的值。这组值称为临界或否定区域。通常,单侧检验有一个临界值,双侧检验有两个临界值。在临界值处,当原假设为真时,检验统计量在检验的否定区域中有值的概率等于显著性水平(用 α 或 alpha 表示)。
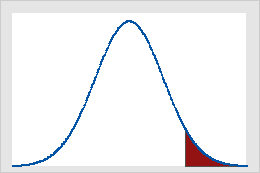
图 A
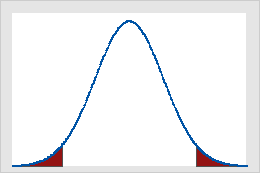
图 B
α = .0.05 时的标准正态分布上的临界值
图 A 显示当检验统计量的值等于或大于 1.64(本例中的临界值)时,单尾 Z 检验的结果显著。阴影面积表示曲线下方面积出现类型 I 错误的概率(在本例中,α = 5%)。图 B 显示当检验统计量的绝对值等于或大于 1.96(本例中的临界值)时,双尾 Z 检验的结果显著。两个阴影面积加在一起等于曲线下方面积的 5% (α)。
计算临界值的示例
在假设检验中,可通过两种方法来确定样本中是否有足够的证据来否定 H0 或无法否定 H0。最常用的方法是将 p 值与预先指定的 α 值(α 是在 H0 为真时否定 H0 的概率)进行比较。但是,有个等效方法是将基于数据计算的检验统计量值与临界值进行比较。下面的示例说明如何计算单样本 t 检验和单因子方差分析的临界值。
为单样本 t 检验计算临界值
假定要针对十个观测值执行单样本 t 检验,进行双侧备择假设(即,H1 不等于),并且使用的 alpha 等于 0.10:
- 选择。
- 选择逆累积概率。
- 在自由度中,输入 9(观测值个数减去 1)。
- 在输入常量中,输入 0.95(1 减去 alpha 的一半)。
这会得出逆累积概率,该值等于临界值 1.83311。如果 t 统计量的绝对值大于此临界值,则可以在显著性水平为 0.10 时否定原假设 H0。
计算方差分析(单因子方差分析)的临界值
假定要针对十二个观测值执行单因子方差分析,该因子有三个水平,并且使用的 alpha 等于 .0.05:
- 选择。
- 选择逆累积概率。
- 在分子自由度中,输入 2(因子水平数减去 1)。
- 在分母自由度中,输入 9(误差的自由度)。
- 在输入常量中,输入 0.95(1 减去 alpha)。
这会得出逆累积概率(即临界值)等于 4.25649。如果 F 统计量大于此临界值,则可以在显著性水平为 0.05 时否定原假设 H0。
