置信区间是从样本统计量派生的值范围,可能包含未知总体参数的值。由于置信区间具有随机性,因此来自特定总体的两个样本将不可能生成相同的置信区间。但是,如果您将样本重复多次,则在所生成的置信区间中有特定百分比的置信区间将包含未知总体参数。
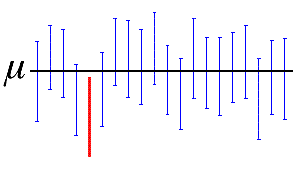
此处,水平黑线表示未知总体均值 µ 的固定值。与水平线相交的垂直蓝色置信区间包含总体均值。完全位于水平线下方的红色置信区间则不包含总体均值。95% 置信区间表明,在来自同一个总体的 20 个样本中,有 19 个样本将生成包含总体参数的置信区间。
使用置信区间可以评估总体参数的估计值。例如,制造商想要知道他们生产的铅笔的平均长度是否不同于目标长度。制造商随机抽取铅笔样本,并确定样本的平均长度为 52 毫米,95% 置信区间为 (50,54)。因此,所有铅笔的平均长度介于 50 毫米和 54 毫米之间的可信度为 95%。
置信区间可通过计算点估计值并确定其边际误差来确定。
- 点估计
- 此单个值通过使用样本数据来估计总体参数。
- 边际误差
-
当您使用统计量来估计值时,一定要记住,无论您的研究设计得有多好,估计值都会受到随机抽样误差的影响。边际误差对这种误差进行量化并指示估计值的精度。
您可能已经了解边际误差,因为它与调查结果相关。例如,政治民意调查可能报告候选人的支持率是 55%,边际误差为 5%。这意味着真正的支持率为 +/- 5%,介于 50% 和 60% 之间。
对于双侧置信区间,边际误差是估计的统计量到每个置信区间值的距离。如果置信区间是对称的,则边际误差是置信区间宽度的一半。例如,凸轮轴的平均估计长度为 600 毫米,置信区间的范围是从 599 到 601。边际误差为 1。
边际误差越大,区间越宽,对于点估计值越不确信。
