在评估两个变量之间的关系时,确定变量之间的相关方式很重要。线性关系是最常见的,但是变量之间还可能具有非线性或单调关系,如下所示。变量之间也有可能没有关系。您应当从创建变量的散点图开始以评估变量之间的关系。
线性关系是可以用直线为其建模的数据趋势。例如,假设一家航空公司想要估计燃油价格对飞行成本的影响。他们发现,一加仑航空燃料每上升一美元,他们的 LA-NYC 航班的飞行成本就增加 3500 美元。这就说明航空燃料成本与飞行成本之间存在线性关系。
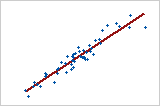
图 1:强正向线性关系
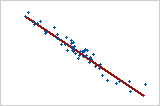
图 2:强负向线性关系
当两个变量以恒定速率同时上升或下降时,存在正向线性关系。图 1 中的点紧靠着直线,表明变量之间存在强关系。此关系的 Pearson 相关系数为 +0.921。
当一个变量上升而另一个变量下降时,存在负向线性关系。图 2 中的点紧靠着直线,表明变量之间存在强关系。此关系的 Pearson 相关系数为 −0.968。
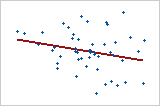
图 3:弱线性关系
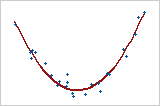
图 4:非线性关系
图 3 中的数据点随机分布。它们不位于直线的附近,这表明如果关系存在,也是非常弱的关系。此关系的 Pearson 相关系数为 −0.253。
如果两个变量之间的关系不是线性的,则上升速率或下降速率可能会随着一个变量变化而变化,这会导致数据中出现“曲线模式”。此曲线趋势可以用非线性函数(如二次函数或三次函数)进行更好的建模,也可以转换为线性关系。图 4 显示两个变量之间的强关系。但是,由于关系不是线性的,因此 Pearson 相关系数仅为 +0.244。此关系说明了在研究可能存在的任何关系时绘制数据图的重要性。
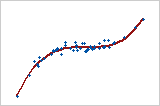
图 5:单调关系
在单调关系中,变量倾向于沿着相同的相对方向移动,但不一定以恒定的速率移动。在线性关系中,变量沿着相同的方向以恒定的速率移动。图 5 显示两个变量同时上升,但不以相同的速率上升。此关系是单调的,但不是线性的。这些数据的 Pearson 相关系数是 0.843,但 Spearman 相关系数较高,为 0.948。
线性关系也是单调关系。例如,图 1 中所示的关系既是单调关系,也是线性关系。
