Minitab® 支持

解释存储描述性统计量的所有统计量

了解关于 Minitab 的更多信息
请查找定义和解释指导，了解随存储描述性统计量提供的每个统计量。

关于本主题

均值

均值是数据的平均值，即所有观测值之和除以观测值的个数。

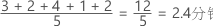
例如，银行五位客户的等待时间（以分钟计）为：3、2、4、1 和 2。平均等待时间按如下公式计算：
即一个客户平均要等待 2.4 分钟才能获得服务。

解释

使用均值来描述具有表示数据中心的单个值的样本。很多统计分析使用均值作为数据分布中心的一个标准度量。

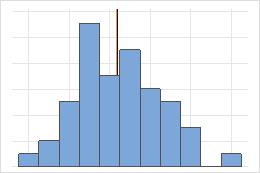
中位数和均值均测量中心趋势。但是，不寻常的值（称为异常值）对中位数的影响会小于它们对均值的影响。如果数据是对称的，则均值和中位数相似。
对称
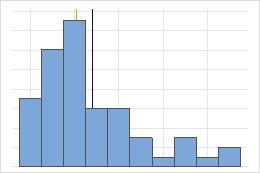
非对称

对于对称分布，均值（蓝线）和中位数（橙线）非常相似，以至于您很难区分这两条线。但是，非对称分布会向右偏斜。

均值的标准误

均值的标准误（SE 均值）估计样本均值之间的变异性，样本均值是在对相同总体重复抽样的情况下获得的。而均值的标准误估计样本之间的变异性，标准差度量单个样本内的变异性。

例如，根据 312 个交货时间的随机样本，得到平均交货时间为 3.80 天，标准差为 1.43 天。这些数字产生的均值标准误为 0.08 天（1.43 除以 312 的平方根）。如果从相同总体中抽取大小相同的多个随机样本，则这些不同样本均值的标准差将大约为 0.08 天。

解释

使用均值的标准误可以确定样本均值对总体均值的估计精确度。

均值的标准误越小，对总体均值的估计越精确。通常，标准差越大，均值的标准误就越大，对总体均值的估计也越不精确。样本越大，均值的标准误就越小，对总体均值的估计也越精确。

Minitab 使用均值的标准误来计算置信区间。

标准差

标准差是离差的最常用度量，即数据从均值展开的程度。符号 σ（西格玛）通常用于表示总体的标准差，而 s 用于表示样本的标准差。对某一过程而言随机或合乎自然规律的变异通常称为噪声。对某一过程而言随机或合乎自然规律的变异通常称为噪声。

由于标准差与数据采用相同的单位，因此它通常比方差更易于解释。

解释

使用标准差可以确定数据从均值扩散的程度。 标准差值越大，数据越分散。 对于正态分布来说，好的经验法则是大约 68% 的值位于均值的一个标准差范围内，95% 的值位于两个标准差范围内，99.7% 的值位于三个标准差范围内。

使用标准差还可以建立用来估计过程的总体变异性的基准。
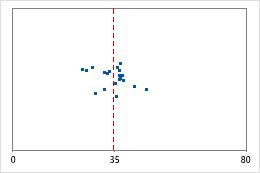
医院 1
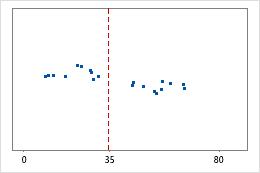
医院 2
医院出院时间

管理员对两家医院急诊部所治疗的患者的出院时间进行跟踪。尽管平均出院时间大致相同（35 分钟），但标准差显著不同。医院 1 的标准差大约为 6。平均而言，患者的出院时间大约偏离均值（虚线）6 分钟。医院 2 的标准差大约为 20。

方差

方差度量数据围绕其均值的分散程度。方差等于标准差的平方。

解释

方差越大，数据越分散。

由于方差 (σ2) 是量的平方，因此其单位也是平方的，这在实际讨论中容易使人混淆。由于标准差与数据采用相同的单位，因此它通常更易于解释。例如，在公共汽车站等待时间样本的均值为 15 分钟，方差为 9 分钟2。由于方差与数据采用不同的单位，所以方差通常会显示为其平方根，即标准差。方差 9 分钟2 等效于标准差 3 分钟。

变异系数

变异系数（用 COV 表示）度量散布，散布描述数据相对于均值的变异程度。变异系数在经过调整后，值将采用无单位刻度。由于进行了此调整，可以使用变异系数（而非标准差）来比较数据中具有不同单位或具有迥异均值的变异性。

解释

变异系数越大，数据越分散。

例如，您是牛奶瓶装厂的质量控制检查员，瓶装厂负责将牛奶装入小瓶和大瓶容器中。您针对每种产品抽取一个样本，并观测到小容器的平均容量为 1 杯（标准差为 0.08 杯），大容器的平均容量为 1 加仑（16 杯，标准差为 0.4 杯）。尽管大容器的标准差是小容器的标准差的 5 倍，但是变异系数支持一个不同的结论。
大容器 小容器
COV = 100 * 0.4 杯 / 16 杯 = 2.5 COV = 100 * 0.08 杯 / 1 杯 = 8
小容器的变异系数是大容器的变异系数的三倍多。换句话说，尽管大容器的标准差大，但小容器的变异系数远大于其均值。

第一个四分位数

四分位数是三个值：第一个四分位数 (Q1) 在 25% 处，第二个四分位数（Q2 或中位数）在 50% 处，第三个四分位数 (Q3) 在 75% 处，这会将排序数据的样本四等分。

第一个四分位数是第 25 个百分位数，它指示有 25% 的数据小于或等于此值。

对于此排序数据，第一个四分位数 (Q1) 是 9.5。也就是说，有 25% 的数据小于或等于 9.5。

中位数

中位数是数据集的中点。在此中点值所在的点上，有一半的观测值大于中点值，有一半的观测值小于中点值。中位数是通过对观测值排秩并在秩顺序中查找第 [N + 1] / 2 位的观测值来确定的。如果观测值数为偶数，则中位数是排在第 N / 2 位和第 [N / 2] + 1 位的观测值的平均值。

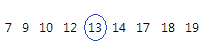
对于此排序数据，中位数是 13。也就是说，一半的值小于或等于 13，一半的值大于或等于 13。如果添加另一个等于 20 的观测值，则中位数为 13.5，即第 5 个观测值 (13) 和第 6 个观测值 (14) 的平均值。

解释

中位数和均值均测量中心趋势。但是，不寻常的值（称为异常值）对中位数的影响会小于它们对均值的影响。如果数据是对称的，则均值和中位数相似。
对称
非对称

对于对称分布，均值（蓝线）和中位数（橙线）非常相似，以至于您很难区分这两条线。但是，非对称分布会向右偏斜。

第三个四分位数

四分位数是三个值：第一个四分位数 (Q1) 在 25% 处，第二个四分位数（Q2 或中位数）在 50% 处，第三个四分位数 (Q3) 在 75% 处，这会将排序数据的样本四等分。

第三个四分位数是第 75 个百分位数，它指示有 75% 的数据小于或等于此值。

对于此排序数据，第三个四分位数 (Q3) 是 17.5。也就是说，有 75% 的数据小于或等于 17.5。

四分位间距

四分位间距 (IQR) 是第一个四分位数 (Q1) 和第三个四分位数 (Q3) 之间的距离。有 50% 的数据位于此间距内。

对于此排序数据，四分位间距是 8 (17.5–9.5 = 8)。也就是说，中间 50% 的数据介于 9.5 和 17.5 之间。

解释

使用四分位间距可以描述数据的散布。数据越分散，四分位间距越大。

截尾均值

数据的均值，不包括最高 5% 和最低 5% 的值。

使用截尾均值可以消除非常大或非常小的值对均值的影响。当数据中包含异常值时，与均值相比，截尾均值能够更好地度量集中趋势。

和

和是所有数据值的合计。和还用在统计计算中，如用于计算均值和标准差。

最小值

最小值是最小的数据值。

在这些数据中，最小值为 7。

13 17 18 19 12 10 7 9 14

解释

使用最小值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最小值非常低，甚至要考虑数据的中心、散布和形状，请调查出现极端值的原因。

最大值

最大值是指最大的数据值。

在这些数据中，最大值为 19。

13 17 18 19 12 10 7 9 14

解释

使用最大值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最大值非常高，甚至要考虑数据的中心、散布和形状，请调查出现极端值的原因。

极差

极差是样本中的最大数据值与最小数据值之差。极差表示包含所有数据值的区间。

解释

使用极差可以了解数据的离差量。较大的极差值表示数据的离差较大。较小的极差值表示数据的离差较小。由于极差仅使用两个数据值进行计算，因此它对于小数据集更有用。

SSQ

未校正平方和是列中每个值的平方之和。例如，如果列中包含 x1, x2, ... , xn，则平方和等于 (x12 + x22 + ... + xn2)。与校正平方和不同的是，未校正平方和包括误差。在对数据值求平方之前不会先减去均值。

偏度

偏度是数据的不对称程度。

解释

使用偏度可帮助您初步了解数据。
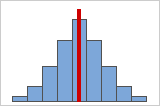
图 A
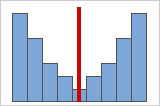
图 B
对称或非偏斜分布

当数据变得更加对称时，它的偏度值会接近零。图 A 显示正态分布的数据，顾名思义，正态分布数据的偏度相对较小。通过沿着此正态数据直方图的中间绘制一条直线，可以很容易地看到两侧，一侧镜像到另一侧。但是，仅缺乏偏度并不能说明正态性。在图 B 显示的分布中，一侧镜像到另一侧，但数据完全不是正态分布。

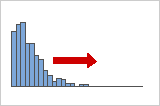
正偏斜或向右偏斜分布

正偏斜或向右偏斜的数据之所以这样命名，是因为分布的“尾部”指向右侧，而且它的偏度值大于 0（或为正数）。薪金数据通常按这种方式偏斜：一家公司中许多员工的薪金相对较低，而少数人员的薪金则非常高。

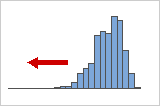
负偏斜或向左偏斜分布

向左偏斜或负偏斜的数据之所以这样命名，是因为分布的“尾部”指向左侧，而且它生成负数偏度值。故障率数据通常向左偏斜。以灯泡为例：极少的灯泡会立即烧坏，大部分灯泡都会持续相当长的时间。

峰度

峰度表示分布的尾部与正态分布的区别。

解释

使用峰度可帮助您初步了解有关数据分布的一般特征。
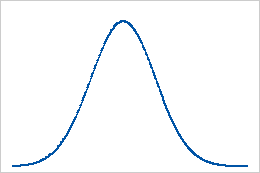
基线：峰度值 0

正态分布的数据为峰度建立了基准。峰度值为 0 表明数据服从完美的正态分布。如果峰度值显著偏离 0，则表明数据不服从正态分布。

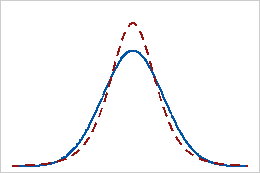
正峰度

具有正峰度值的分布表明，相比于正态分布，该分布有更重的尾部。例如，服从 t 分布的数据具有正峰度值。实线表示正态分布，虚线表示具有正峰度值的分布。

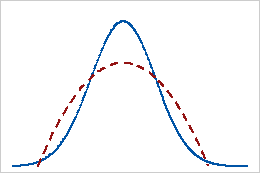
负峰度

具有负峰度值的分布表明，相比于正态分布，该分布有更轻的尾部。例如，服从 Beta 分布（第一个和第二个分布形状参数等于 2）的数据具有负峰度值。实线表示正态分布，虚线表示具有负峰度值的分布。

MSSD

MSSD 是均方递差。MSSD 是方差的估计值。MSSD 的一个可能用法是检验一系列观测值是否随机。在质量控制中，MSSD 的一个可能用法是在子组大小为 1 时估计方差。

N

样本中非缺失值的个数。

在该示例中，记录了 141 个观测值。
总数 N N*
149 141 8

N 缺失

样本中缺失值的个数。缺失值个数是指包含缺失值符号 * 的单元格数。

在该示例中，数据收集期间出现 8 个错误，这些错误记录为缺失值。
总计数 N N 缺失
149 141 8

计数

列中观测值的总数。用于表示 N 缺失和 N 非缺失之和。

在该示例中，有 141 个有效的观测值，8 个缺失值。计数为 149。
计数 N N 缺失
149 141 8

CumN

累积 N 是连续类别中观测值个数的累计。例如，小学记录一到六年级的学生数。CumN 列包含学生总体的累积计数：
年级 计数 CumN 计算
1 49 49 49
2 58 107 49 + 58
3 52 159 49 + 58 + 52
4 60 219 49 + 58 + 52 + 60
5 48 267 49 + 58 + 52 + 60 + 48
6 55 322 49 + 58 + 52 + 60 + 48 + 55

百分比

“按变量”的每个组中的观测值所占的百分比。在下面的示例中，有四组：第 1 行、第 2 行、第 3 行和第 4 行。

组（按变量） 百分比
第 1 行 16
第 2 行 20
第 3 行 36
第 4 行 28

累积百分比

累积百分比是“按变量”的每个组所占百分比的累积和。在下面的示例中，“按变量”有 4 组：第 1 行、第 2 行、第 3 行和第 4 行。

组（按变量） 百分比 累积百分比
第 1 行 16 16
第 2 行 20 36
第 3 行 36 72
第 4 行 28 100
Copyright © 2024 Minitab, LLC. All rights Reserved.