指定检验,指定显著性水平,然后选择备择假设。
异常值检验
Minitab 的所有异常值检验旨在检测样本中的单个异常值。通常使用 Grubbs 检验即可。但是,如果样本中包含多个潜在的异常值,则 Grubbs 检验和 Dixon Q 比值可能无效。
请勿对数据执行多个异常值检验。如果您执行异常值检验,删除检验所标识的异常值,然后执行第二个异常值检验,则有可能会删除非异常值。为了避免此风险,请选择最适合您的情形的异常值检验类型:
- 如果您不知道数据中是否包括异常值,请使用 Grubbs 检验。
- 如果您知道数据中包括一个或多个异常值,请使用其中一个 Dixon 检验。Dixon 检验旨在克服由多个潜在异常值导致的掩蔽效应。
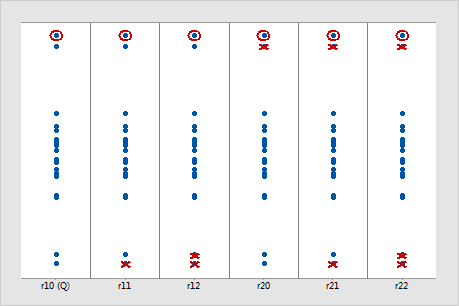
在下图中,每一列都显示 Dixon 比值检验对同一个样本的不同处理方式。带圆圈的值是潜在的异常值。X 指示每个 Dixon 比值检验在计算检验统计量时所忽略的数据值。(此图假定备择假设为最小或最大数据值为异常值或最大数据值为异常值。)对于这些数据,Dixon r22 比值检验最有可能将带圆圈的值标识为异常值。
来自正态总体的样本越大,越有可能包括极端值。Dixon 建议遵循以下针对比值的一般准则。
| 样本数量 (n) | 建议的比值 |
|---|---|
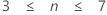 |
r10(又称为 Dixon Q 比值) |
 |
r11 |
 |
r21 |
 |
r22 |
显著性水平
通过比较显著性水平与 p 值可确定是否定原假设还是无法否定原假设 (H0)。如果 p 值小于显著性水平,则通常的解释是结果在统计意义上显著,而且可以否定 H0。
通常,显著性水平(用 α 或 alpha 表示)为 0.05 即可。显著性水平 0.05 指示在实际上不存在差值时得出存在差值的风险为 5%。
- 选择较高的显著性水平(如 0.10)可以更确定地检测到可能存在的任何差值。例如,一位质量工程师将新滚珠轴承的稳定性与当前轴承的稳定性进行比较。该工程师必须高度确信新滚珠轴承的稳定性,因为不稳定的滚珠轴承会导致灾难性后果。该工程师选择 0.10 的显著性水平,以更确定地检测到滚珠轴承稳定性方面任何可能的差异。
- 选择较低的显著性水平(如 0.01)可以更确定地仅检测到一个实际存在的差异。例如,一家制药公司的科学家必须十分确信公司的新药可以显著减轻症状的声明。该科学家选择 0.001 的显著性水平以更加确信任何显著的症状差异的确存在。
您要确定什么(备择假设)?
从您要确定什么(备择假设)?中,选择下面的备择假设检验之一:
- 最小或最大数据值为异常值:在最小数据值或最大数据值可能为异常值时使用此双侧检验。虽然此双侧检验可以检测最小或最大数据值的异常值,但是它比单侧检验的功效要低。
- 最小数据值为异常值:在怀疑最小数据值为异常值时使用此单侧检验。虽然此单侧检验比双侧检验的功效更高,但是它无法检测作为最大数据值的异常值。
- 最大数据值为异常值:在怀疑最大数据值为异常值时使用此单侧检验。虽然此单侧检验比双侧检验的功效更高,但是它无法检测作为最小数据值的异常值。
