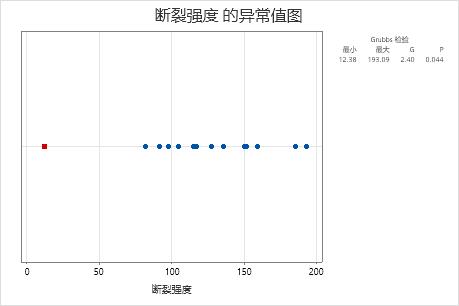
一家木质手柄公司的质量工程师检验了一个扫帚柄随机样本的强度。这位工程师记录了使每根扫帚柄断裂所需的力度。工程师创建了一张包含这些数据的图形,发现样本中似乎存在一个异常小的值。
这位工程师执行了异常值检验,以确定最小的值是否为异常值。
- 打开样本数据,手柄强度.MWX。
- 选择。
- 在变量中,输入断裂强度。
- 单击选项。
- 从您要确定什么(备择假设)?中,选择最小数据值为异常值。
- 在每个对话框中单击确定。
解释结果
样本均值为 123.4。G 统计量指示最小数据值 12.38 比均值小 2.4 个标准差。P 值指示,如果所有的值都确实来自同一个正态分布总体,则获得如此之小的最小值的概率仅为 0.044。由于 p 值 0.044 小于显著性水平 0.05(用 α 或 alpha 表示),因此工程师否定原假设并得出最小值是异常值的结论。
工程师研究和发现意外输入数据的人员键入的是 12.38(而非 123.8)。
方法
| 原假设 | 所有数据值均来自相同的正态总体 |
|---|---|
| 备择假设 | 最小数据值为异常值 |
| 显著性水平 | α = 0.05 |
Grubbs 检验
| 变量 | N | 均值 | 标准差 | 最小 | 最大 | G | P |
|---|---|---|---|---|---|---|---|
| 断裂强度 | 14 | 123.4 | 46.3 | 12.4 | 193.1 | 2.40 | 0.044 |
异常值
| 变量 | 行 | 异常值 |
|---|---|---|
| 断裂强度 | 10 | 12.38 |