请选择您所选的方法或公式。
均值
一批数字的中心的常用度量。均值又称为平均数。均值是由所有观测值之和除以(非缺失)观测值个数得来的。
公式
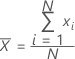
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
| N | 非缺失观测值个数 |
标准差 (StDev)
样本标准差用来度量数据的散布。它等于样本方差的平方根。
公式
如果列中包含 x 1, x 2,..., x N,且均值为  ,则样本的标准差为:
,则样本的标准差为:
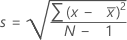
 ,则样本的标准差为:
,则样本的标准差为:
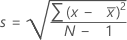
表示法
| 项 | 说明 |
|---|---|
| x i | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
N
Minitab 显示样本中非缺失观测值的个数。
Anderson-Darling 统计量 (A2)
A2 度量拟合线(基于所选分布)与非参数步骤函数(基于标绘点)之间的面积。统计量是在分布的尾部施加更大权重的平方距离。如果 Anderson-Darling 值较小,则表明分布与数据拟合得更好。
Anderson-Darling 正态性检验的定义如下:
H0:数据服从正态分布
H1:数据不服从正态分布
公式

表示法
| 项 | 说明 |
|---|---|
| F(Yi) |  ,即标准正态分布的累积分布函数 ,即标准正态分布的累积分布函数 |
| Yi | 排序数据 |
Ryan-Joiner
Ryan-Joiner 检验提供相关系数,相关系数指示数据和数据的正态评分之间的相关性。如果相关系数接近 1,则说明数据与正态概率图离得很近。如果相关系数小于相应的临界值,则将否定正态性原假设。
公式
相关系数的计算公式如下:
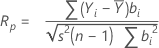
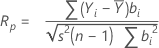
表示法
| 项 | 说明 |
|---|---|
| Yi | 排序观测值 |
| bi | 排序数据的正态评分 |
| s2 | 样本方差 |
Kolmogorov-Smirnov
公式
Kolmogorov-Smirnov 检验的定义如下所示:
- H0:数据服从正态分布
- H1:数据不服从正态分布
Kolmogorov-Smirnov 检验统计量的定义如下所示:


表示法
| 项 | 说明 |
|---|---|
| D+ | maxi {i / n – Z (i)} |
| D– | maxi {Z (i) – (i – 1) / n)} |
| Z | F(X(i)) |
| F(x) | 正态分布的概率分布函数 |
| X(i) | 随机样本的第 i 个顺序统计量,1 ≤ i ≤ n |
| n | 样本数量 |
P 值
P 值是另一个用来报告正态性检验结果的定量度量。如果 p 值较小,则表示原假设为假。
如果您知道 A2,则可以计算 p 值。设:
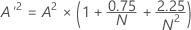
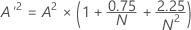
根据 A'2,将使用以下等式计算 p:
- 如果 13 > A'2 > 0.600,则 p = exp(1.2937 - 5.709 * A'2 + 0.0186(A'2)2)
- 如果 0.600 > A'2 > 0.340,则 p = exp(0.9177 - 4.279 * A'2 – 1.38(A'2)2)
- 如果 0.340 > A'2 > 0.200,则 p = 1 – exp(–8.318 + 42.796 * A'2 – 59.938(A'2)2)
- 如果 A'2 <0.200,则 p = 1 – exp(–13.436 + 101.14 * A'2 – 223.73(A'2)2)
标绘点
通常,点越接近拟合线,表明拟合得越好。Minitab 提供两种拟合优度度量来帮助评估分布与数据的拟合程度。
公式
下表显示了如何构造中间线:
| 分布 | x 坐标 | y 坐标 |
|---|---|---|
| 正态 | x | Φ–1 norm |
表示法
| 项 | 说明 |
|---|---|
| Φ–1 norm | 标准正态分布的逆 CDF 为 p 返回的值 |
概率图
输入数据绘制为 x 值。Minitab 计算发生概率而不进行分布假设。图上的 Y 刻度与正态分布论文中的 Y 刻度相似,在正态分布论文中,概率图绘制为一条直线,就好像数据来自正态分布一样。
