A 平方
Anderson-Darling 拟合优度统计量 (A-Squared) 度量拟合线(基于正态分布)和经验分布函数(基于数据点)之间的面积。Anderson-Darling 统计量是在分布的尾部施加更大权重的平方距离。
解释
Minitab 使用 Anderson-Darling 统计量计算 p 值。P 值是一个概率,用来度量否定原假设的证据。P 值越小,否定原假设的证据越充分。Anderson-Darling 统计量的值越小,数据越服从正态分布。
P 值
P 值是一个概率,用来度量否定原假设的证据。P 值越小,否定原假设的证据越充分。
解释
使用 p 值可确定数据是否不服从正态分布。
- P 值 ≤ α:数据不服从正态分布(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设并得出数据不服从正态分布的结论。
- P 值 > α:您无法得出数据不服从正态分布的结论(无法否定 H0)
- 如果 p 值大于显著性水平,则决策为无法否定原假设。您没有足够的证据得出数据不服从正态分布的结论。
均值
均值是数据的平均值,即所有观测值之和除以观测值的个数。
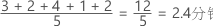
解释
使用均值来描述具有表示数据中心的单个值的样本。很多统计分析使用均值作为数据分布中心的一个标准度量。
对称
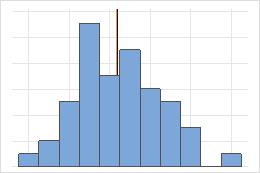
非对称
对于对称分布,均值(蓝线)和中位数(橙线)非常相似,以至于您很难区分这两条线。但是,非对称分布会向右偏斜。
标准差
标准差是离差的最常用度量,即数据从均值展开的程度。符号 σ(西格玛)通常用于表示总体的标准差,而 s 用于表示样本的标准差。对某一过程而言随机或合乎自然规律的变异通常称为噪声。对某一过程而言随机或合乎自然规律的变异通常称为噪声。
由于标准差与数据采用相同的单位,因此它通常比方差更易于解释。
解释
使用标准差可以确定数据从均值扩散的程度。 标准差值越大,数据越分散。 对于正态分布来说,好的经验法则是大约 68% 的值位于均值的一个标准差范围内,95% 的值位于两个标准差范围内,99.7% 的值位于三个标准差范围内。
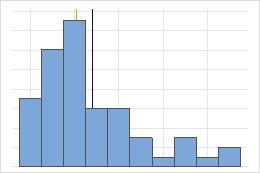
医院 1
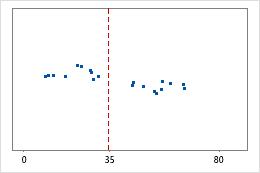
医院 2
医院出院时间
管理员对两家医院急诊部所治疗的患者的出院时间进行跟踪。尽管平均出院时间大致相同(35 分钟),但标准差显著不同。医院 1 的标准差大约为 6。平均而言,患者的出院时间大约偏离均值(虚线)6 分钟。医院 2 的标准差大约为 20。
方差
方差度量数据围绕其均值的分散程度。方差等于标准差的平方。
解释
方差越大,数据越分散。
由于方差 (σ2) 是量的平方,因此其单位也是平方的,这在实际讨论中容易使人混淆。由于标准差与数据采用相同的单位,因此它通常更易于解释。例如,在公共汽车站等待时间样本的均值为 15 分钟,方差为 9 分钟2。由于方差与数据采用不同的单位,所以方差通常会显示为其平方根,即标准差。方差 9 分钟2 等效于标准差 3 分钟。
偏度
偏度是数据的不对称程度。
解释
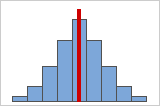
图 A
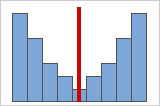
图 B
对称或非偏斜分布
当数据变得更加对称时,它的偏度值会接近零。图 A 显示正态分布的数据,顾名思义,正态分布数据的偏度相对较小。通过沿着此正态数据直方图的中间绘制一条直线,可以很容易地看到两侧,一侧镜像到另一侧。但是,仅缺乏偏度并不能说明正态性。在图 B 显示的分布中,一侧镜像到另一侧,但数据完全不是正态分布。
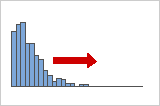
正偏斜或向右偏斜分布
正偏斜或向右偏斜的数据之所以这样命名,是因为分布的“尾部”指向右侧,而且它的偏度值大于 0(或为正数)。薪金数据通常按这种方式偏斜:一家公司中许多员工的薪金相对较低,而少数人员的薪金则非常高。
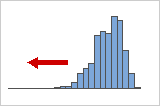
负偏斜或向左偏斜分布
向左偏斜或负偏斜的数据之所以这样命名,是因为分布的“尾部”指向左侧,而且它生成负数偏度值。故障率数据通常向左偏斜。以灯泡为例:极少的灯泡会立即烧坏,大部分灯泡都会持续相当长的时间。
峰度
峰度表示分布的尾部与正态分布的区别。
解释
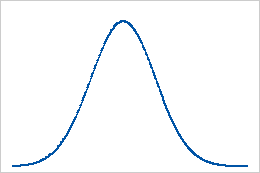
基线:峰度值 0
正态分布的数据为峰度建立了基准。峰度值为 0 表明数据服从完美的正态分布。如果峰度值显著偏离 0,则表明数据不服从正态分布。
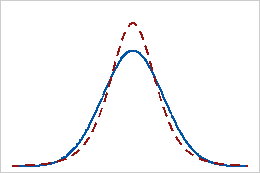
正峰度
具有正峰度值的分布表明,相比于正态分布,该分布有更重的尾部。例如,服从 t 分布的数据具有正峰度值。实线表示正态分布,虚线表示具有正峰度值的分布。
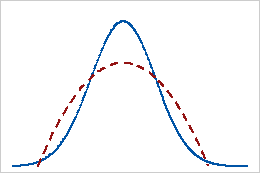
负峰度
具有负峰度值的分布表明,相比于正态分布,该分布有更轻的尾部。例如,服从 Beta 分布(第一个和第二个分布形状参数等于 2)的数据具有负峰度值。实线表示正态分布,虚线表示具有负峰度值的分布。
N
样本中非缺失值的个数。
| 总数 | N | N* |
|---|---|---|
| 149 | 141 | 8 |
最小值
最小值是最小的数据值。
在这些数据中,最小值为 7。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最小值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最小值非常低,甚至要考虑数据的中心、散布和形状,请调查出现极端值的原因。
第一个四分位数
四分位数是三个值:第一个四分位数 (Q1) 在 25% 处,第二个四分位数(Q2 或中位数)在 50% 处,第三个四分位数 (Q3) 在 75% 处,这会将排序数据的样本四等分。
第一个四分位数是第 25 个百分位数,它指示有 25% 的数据小于或等于此值。

对于此排序数据,第一个四分位数 (Q1) 是 9.5。也就是说,有 25% 的数据小于或等于 9.5。
中位数
中位数是数据集的中点。在此中点值所在的点上,有一半的观测值大于中点值,有一半的观测值小于中点值。中位数是通过对观测值排秩并在秩顺序中查找第 [N + 1] / 2 位的观测值来确定的。如果观测值数为偶数,则中位数是排在第 N / 2 位和第 [N / 2] + 1 位的观测值的平均值。
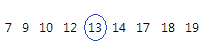
对于此排序数据,中位数是 13。也就是说,一半的值小于或等于 13,一半的值大于或等于 13。如果添加另一个等于 20 的观测值,则中位数为 13.5,即第 5 个观测值 (13) 和第 6 个观测值 (14) 的平均值。
解释

对称

非对称
对于对称分布,均值(蓝线)和中位数(橙线)非常相似,以至于您很难区分这两条线。但是,非对称分布会向右偏斜。
第三个四分位数
四分位数是三个值:第一个四分位数 (Q1) 在 25% 处,第二个四分位数(Q2 或中位数)在 50% 处,第三个四分位数 (Q3) 在 75% 处,这会将排序数据的样本四等分。
第三个四分位数是第 75 个百分位数,它指示有 75% 的数据小于或等于此值。

对于此排序数据,第三个四分位数 (Q3) 是 17.5。也就是说,有 75% 的数据小于或等于 17.5。
最大值
最大值是指最大的数据值。
在这些数据中,最大值为 19。
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
解释
使用最大值可以标识可能的异常值或数据输入错误。评估数据散布最简单的方法之一就是比较最小值和最大值。如果最大值非常高,甚至要考虑数据的中心、散布和形状,请调查出现极端值的原因。
置信区间
置信区间提供总体参数的可能值范围。由于样本的随机性,来自总体的两个样本不可能生成相同的置信区间。但是如果将样本重复许多次,则所获得的特定百分比的置信区间或限值会包含未知的总体参数。这些包含参数的置信区间或限值的百分比是区间的置信水平。例如,95% 置信水平表明,如果从总体中随机抽取 100 个样本,则大约 95 个样本将产生包含总体参数的区间。
上限定义可能大于总体参数的值。下限定义可能小于总体参数的值。
置信区间有助于评估结果的实际意义。使用您的专业知识可以确定置信区间是否包括对您的情形有实际意义的值。如果区间因太宽而毫无用处,请考虑增加样本数量。有关更多信息,请转到获得更加精确的置信区间的方法。
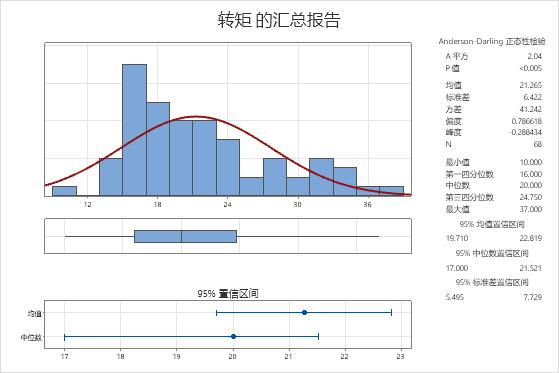
- The population mean for the torque measurements is between 19.710 and 22.819.
- The population median for the torque measurements is between 17 and 21.521.
- The population standard deviation for the torque measurements is between 5.495 and 7.729.
直方图
直方图将样本值分成许多区间,并使用条形表示每个区间中的数据值的频率。
解释
可使用直方图评估数据的形状和散布。 当样本数量大于 20 时,直方图具有最佳状态。
- 偏斜数据
-
可以使用与正态曲线重叠的数据直方图来检查数据的正态性。正态分布是对称的,并且呈钟形,如曲线所示。通常很难评估小样本的正态性。概率图最适用于确定分布拟合。
良好拟合
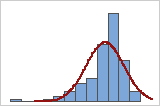
不良拟合
- 异常值
-
异常值,是远离其他数据值的数据值,可以显著影响您的分析结果。通常情况下,在箱线图上最容易识别异常值。
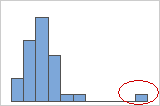
在直方图上,图形任一端上的孤立条形标识可能的异常值。
尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除异常、单次事件(也称为特殊原因)的数据值。然后,重新执行分析。有关更多信息,请转到 标识异常值。
- 多模态数据
-
多模态数据具有多个峰值,也称为模式。多模态数据往往表明未考虑到重要变量。
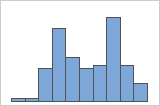
简单
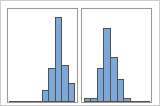
含组
例如,一位银行经理收集等待时间数据,并创建一个简单的直方图。该直方图具有两个峰值。经过进一步调查,该经理确定:兑现支票的客户的等待时间短于申请房屋净值贷款的客户的等待时间。经理为客户任务添加一个组变量,然后创建一个包含该组的直方图。
如果您具有其他信息以用于将观测值分类到组,则可以创建一个包含此信息的组变量。然后,可以创建其中含有组的图形,以确定组变量是否导致数据中的峰值。
箱线图
箱线图提供了样本分布的图形汇总。箱线图显示数据的形状、集中趋势和变异性。
解释
可使用箱线图检查数据的散布,以及确定任何可能的异常值。 当样本数量大于 20 时,箱线图具有最佳状态。
- 偏斜数据
-
检查数据的散布以确定数据看上去是否偏斜。当数据偏斜时,大多数数据位于图形的高或低侧。通常情况下,在直方图或箱线图中最易于检测偏度。
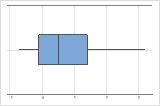
右偏斜
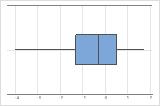
左偏斜
带右偏斜数据的箱线图显示等待时间。大部分等待时间相对较短,只有少数等待时间很长。带左偏斜数据的箱线图显示故障时间数据。有几个项目立即失败,还有其他许多项目在随后失败。
- 异常值
-
异常值,是远离其他数据值的数据值,可以显著影响您的分析结果。通常情况下,在箱线图上最容易识别异常值。
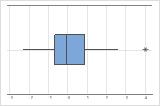
在箱线图上,星号 (*) 表示异常值。
尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除异常、单次事件(也称为特殊原因)的数据值。然后,重新执行分析。有关更多信息,请转到 标识异常值。
