关于本主题
均值
一批数字的中心的常用度量。均值又称为平均数。均值是由所有观测值之和除以(非缺失)观测值个数得来的。
公式
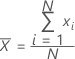
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
| N | 非缺失观测值个数 |
均值的标准误(均值标准误)
均值的标准误等于标准差除以样本数量的平方根。
公式

表示法
| 项 | 说明 |
|---|---|
| s | 样本的标准差 |
| N | 非缺失观测值个数 |
标准差 (StDev)
样本标准差用来度量数据的散布。它等于样本方差的平方根。
公式
 ,则样本的标准差为:
,则样本的标准差为:
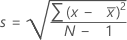
表示法
| 项 | 说明 |
|---|---|
| x i | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
方差
方差度量数据围绕其均值的分散程度。方差等于标准差的平方。
公式
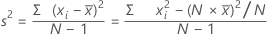
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
变异系数 (CoefVar)
变异系数可度量用百分比计算的相对变异性。
公式

Minitab 按如下公式计算它:

表示法
| 项 | 说明 |
|---|---|
| s | 样本的标准差 |
 | 观测值的均值 |
第一个四分位数 (Q1)
25% 的样本观测值小于或等于第一个四分位数的值。因此,第一个四分位数又称为第 25 个百分位数。
公式

表示法
| 项 | 说明 |
|---|---|
| 是 | w 的整数截断值 |
| w | 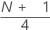 |
| z | w 的已被截断的分数分量 |
| xj | 样本数据列表中的第 j 个观测值,按从小到大的顺序排列 |
注意
当 w 是整数时,y = w、z = 0、Q1 = xy。
中位数
样本中位数位于数据的中间:至少有一半的观测值小于或等于它,至少有一半的观测值大于或等于它。
假设您有一个包含 N 个值的列。要计算中位数,首先按照从小到大的顺序对数据值进行排序。如果 N 为奇数,则样本中位数是位于中间的值。如果 N 为偶数,则样本中位数是两个中间值的平均数。
例如,当 N = 5 且您有数据 x1、x2、x3、x4 和 x5 时,中位数 = x3。
当 N = 6 且您有排序数据 x1、x2、x3、x4、x5 和 x6 时:

其中 x3 和 x4 是第三个和第四个观测值。
第三个四分位数 (Q3)
75% 的样本观测值小于或等于第三个四分位数的值。因此,第三个四分位数又称为第 75 个百分位数。
公式

表示法
| 项 | 说明 |
|---|---|
| 是 | w 的截断值 |
| w |
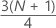 |
| z | w 的已被截断的分数分量 |
| xj | 样本数据列表中的第 j 个观测值,按从小到大的顺序排列 |
注意
当 w 是整数时,y = w、z = 0、Q3 = xy。
四分位间距 (IQR)
四分位间距等于第三个四分位数减去第一个四分位数。
众数
众数是数据集内出现频率最高的数据值。如果存在多个众数,Minitab 将显示最小的众数,最多显示四个。用于众数的 N 是指一个或多个众数出现的次数。
截尾均值 (TrMean)
Minitab 通过以下方法计算截尾均值:去掉最小 5% 和最大 5% 的值(圆整到最近的整数),然后计算剩余值的均值。
和
公式

表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
最小值
数据集中的最小值。
最大值
数据集中的最大值。
极差
极差是最大数据值与最小数据值之差。
R = 最大值 – 最小值
平方和
Minitab 对该列中的每个值求平方,然后计算这些平方值的和。
公式
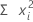
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
偏度
偏度用来度量不对称度。负值表示向左偏斜,正值表示向右偏斜。零值不一定表示对称。
公式
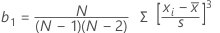
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
| s | 样本的标准差 |
峰度
峰度可用来度量某个分布与正态分布的差异程度。正值通常表示,相比于正态分布,该分布的波峰更陡。负值表示,相比于正态分布,该分布的波峰更平坦。
公式

表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
 | 观测值的均值 |
| N | 非缺失观测值个数 |
| s | 样本的标准差 |
MSSD(均方递差)
Minitab 计算一批数字的一半 MSSD(均方递差)。对于这些递差将求平方并对平方值求和。Minitab 随后会将结果除以 2 并计算平均数。
公式
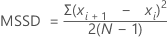
表示法
| 项 | 说明 |
|---|---|
| xi | 第 i 个观测值 |
 | 观测值的均值 |
N 非缺失 (N)
样本中非缺失值的个数。
N 缺失 (N*)
样本中缺失值的个数。缺失值个数是指包含缺失值符号 * 的单元格数。
N 合计(总数)
列中观测值的总数。
百分比
Minitab 计算每个组占整体的百分比。
公式
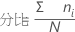
表示法
| 项 | 说明 |
|---|---|
| ni | 第 i 组中的观测值个数 |
| N | 非缺失观测值个数 |
累积百分比 (CumPct)
Minitab 计算由每个组表示的累积百分比。
公式
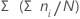
表示法
| 项 | 说明 |
|---|---|
| ni | 第 i 组中的观测值个数 |
| N | 非缺失观测值个数 |
