步骤 1:描述样本的数量
使用 N 可以知道样本中有多少个观测值。Minitab 在该计数中不包括缺失值。
您不应当收集数量较小的数据样本。至少包含 20 个观测值的样本通常足以表示数据的分布。但是,为了更好地使用直方图表示分布,一些业内人员建议您至少有 50 个观测值。样本越大,提供的过程参数估计值(如均值和标准差)越精确。
统计量
| 变量 | N | N* | 均值 | 均值标准误 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|---|---|
| 转矩 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要结果:N
在这些结果中,有 68 个观测值。
步骤 2:描述数据的中心
使用均值来描述具有表示数据中心的单个值的样本。很多统计分析使用均值作为数据分布中心的一个标准度量。
中位数是数据分布中心的另一个度量。中位数受异常值的影响通常比均值要小。一半的数据值大于中位数值,一半的数据值小于中位数值。
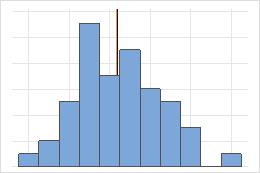
对称
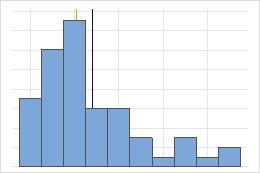
非对称
对于对称分布,均值(蓝线)和中位数(橙线)非常相似,以至于您很难区分这两条线。但是,非对称分布会向右偏斜。
统计量
| 变量 | N | N* | 均值 | 均值标准误 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|---|---|
| 转矩 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要结果:均值和中位数
在这些结果中,去除牙膏盖所需的转矩均值为 21.265,转矩中位数是 20。数据似乎向右偏斜,这解释了均值大于中位数的原因。
步骤 3:描述数据的散布
使用标准差可以确定数据从均值扩散的程度。 标准差值越大,数据越分散。
统计量
| 变量 | N | N* | 均值 | 均值标准误 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|---|---|
| 转矩 | 68 | 0 | 21.2647 | 0.778784 | 6.42202 | 10 | 16 | 20 | 24.75 | 37 |
主要结果:标准差
在这些结果中,标准差是 6.422。对于正态数据来说,大多数观测值分散于均值每一侧 3 个标准差内。
步骤 4:评估数据分布的形状和散布
可使用直方图、单值图和箱线图评估数据的形状和散布,还可以确定任何可能的异常值。
检查数据的散布以确定数据看上去是否偏斜
当数据偏斜时,大多数数据位于图形的高或低侧。通常情况下,在直方图或箱线图中最易于检测偏度。
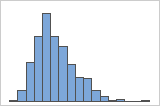
右偏斜
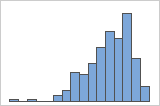
左偏斜
带右偏斜数据的直方图显示等待时间。大部分等待时间相对较短,只有少数等待时间很长。带左偏斜数据的条形图显示故障时间数据。有几个项目立即失败,还有其他许多项目在随后失败。
确定数据的变化量
评估点的散布情况,以确定样本的变异程度。样本的变异程度越大,越多点从远离数据中心散布。

此单值图显示右侧数据比左侧数据的变异程度大。
查找多模态数据
多模态数据具有多个峰值,也称为模式。多模态数据往往表明未考虑到重要变量。
如果您具有其他信息以用于将观测值分类到组,则可以创建一个包含此信息的组变量。然后,可以创建其中含有组的图形,以确定组变量是否导致数据中的峰值。
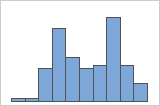
简单
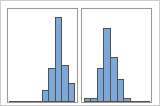
含组
例如,一位银行经理收集等待时间数据,并创建一个简单的直方图。该直方图具有两个峰值。经过进一步调查,该经理确定:兑现支票的客户的等待时间短于申请房屋净值贷款的客户的等待时间。经理为客户任务添加一个组变量,然后创建一个包含该组的直方图。
标识异常值
异常值,是远离其他数据值的数据值,可以显著影响您的分析结果。通常情况下,在箱线图上最容易识别异常值。
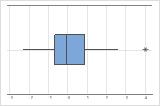
在箱线图上,星号 (*) 表示异常值。
尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除异常、单次事件(也称为特殊原因)的数据值。然后,重新执行分析。有关更多信息,请转到 标识异常值。
步骤 5:比较来自不同组的数据
如果您有一个用来标识数据中各个组的按变量,则可以使用它来按组或按组水平分析数据。
统计量
| 变量 | 机器 | N | N* | 均值 | 均值标准误 | 标准差 | 最小值 | 下四分位数 | 中位数 | 上四分位数 | 最大值 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 转矩 | 1 | 36 | 0 | 18.6667 | 0.732467 | 4.39480 | 10 | 15.25 | 17 | 21.75 | 30 |
| 2 | 32 | 0 | 24.1875 | 1.25839 | 7.11852 | 14 | 17.5 | 24 | 31 | 37 |
在这些结果中,汇总统计量是按机器单独计算的。您可以方便地查看每台机器的中心差值和数据散布。例如,机器 1 的平均转矩和变异性比机器 2 小。要确定均值差值是否显著,可以执行双样本 t 检验。
