请完成以下步骤来解释相关分析。主要输出包括 Pearson 相关系数、Spearman 相关系数和 p 值。
步骤 1:检查矩阵图上变量之间的关系
步骤 1:使用矩阵图检查两个连续变量之间的关系。还要在关系中查找异常值。异常值可能会严重影响 Pearson 相关系数的结果。
确定关系是线性关系、单调关系还是二者都不是。下面是相关系数所描述之形式类型的示例。Pearson 相关系数适用于线性形式。Spearman 相关系数适用于单调形式。

无关系
点随机落在图上,表明变量之间无线性关系。
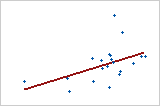
中等正向关系
一些点靠近直线,另一些点远离直线,仅表明变量之间存在中等线性关系。
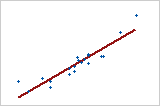
大正向关系
点靠近线,表明变量之间存在强大的线性关系。关系为正向,因为当一个变量上升时,另一个变量也会上升。
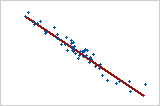
大负向关系
点靠近线,表明变量之间存在强大的负向关系。关系为负向,因为当一个变量上升时,另一个变量会下降。
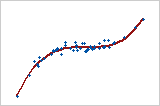
单调
在单调关系中,变量倾向于沿着相同的相对方向移动,但不一定以恒定的速率移动。在线性关系中,变量沿着相同的方向以恒定的速率移动。此图显示两个变量同时上升,但不以相同的速率上升。此关系是单调的,但不是线性的。这些数据的 Pearson 相关系数是 0.843,但 Spearman 相关系数较高,为 0.948。
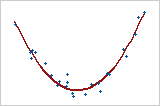
二次曲线
此示例显示曲线关系。即使变量之间的关系很强,相关系数也将接近于零。关系既不是线性的又不是单调的。
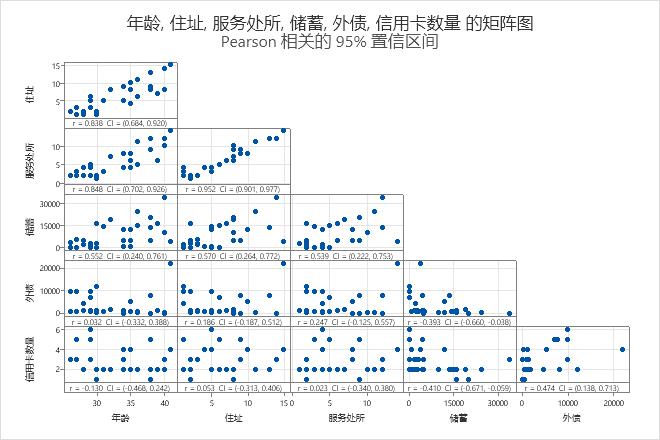
主要结果:矩阵图
在这些结果中,您可以查看正向线性关系、负向线性关系、可能的曲线关系和几个异常值。
- 聘用年限与居住年限之间存在强正向线性关系。
- 信用卡数与储蓄之间存在弱负向线性关系。
- 负债似乎具有异常值,需要进行调查。
步骤 2:检查变量之间的相关系数
使用 Pearson 相关系数可以检查两个连续变量之间线性关系的强度和方向。
- 强度
-
相关系数可以是介于 −1 到 +1 之间的值。系数的绝对值越大,变量之间的关系越强。
对于 Pearson 相关性,绝对值 1 指示完美的线性关系。接近 0 的相关系数表示变量之间无线性关系。 - 方向
-
系数的符号表示关系的方向。如果两个变量都倾向于同时上升或下降,则系数为正,代表相关的直线向上倾斜。如果一个变量倾向于在另一个变量下降时上升,则系数为负,代表相关的直线向下倾斜。
在解释相关系数时,请考虑以下几点:
- 仅根据相关即得出一个变量会导致另一个变量更改的结论绝对不合适。只有进行过适当控制的试验才能确定是否存在因果关系。
- Pearson 相关系数对极端数据值非常敏感。数据集中与其他值截然不同的单个值会极大地改变该系数值。您应该尝试找出导致任何极端值的原因。更正任何数据输入错误或测量误差。考虑删除与异常的单次事件(也称为特殊原因)相关联的数据值。然后,重新执行分析。
- Pearson 相关系数低并不意味着变量之间不存在关系。变量之间可能存在非线性关系。
相关: 年龄, 住址, 服务处所, 储蓄, 外债, 信用卡数量
方法
| 相关类型 | Pearson |
|---|---|
| 已使用的行数 | 30 |
相关
| 年龄 | 住址 | 服务处所 | 储蓄 | 外债 | |
|---|---|---|---|---|---|
| 住址 | 0.838 | ||||
| 服务处所 | 0.848 | 0.952 | |||
| 储蓄 | 0.552 | 0.570 | 0.539 | ||
| 外债 | 0.032 | 0.186 | 0.247 | -0.393 | |
| 信用卡数量 | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
主要结果:Pearson 相关
居住年限与年龄、聘用年限与年龄、聘用年限和居住年限之间存在正向线性关系。这些对的 Pearson 相关系数为:
- 居住年限与年龄:0.838
- 聘用年限与年龄:0.848
- 聘用年限与居住年限:0.952
对于以下各对存在负向线性关系,它们的 Pearson 相关系数为负:
- 负债与储蓄:−0.393
- 信用卡数与年龄:−0.130
- 信用卡数与储蓄:−0.410
