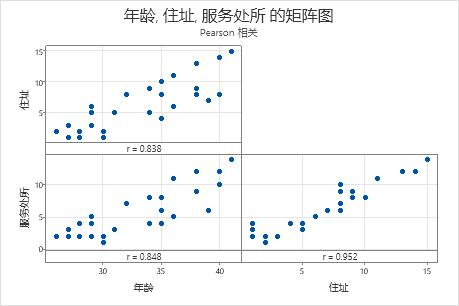
Pearson 相关
相关矩阵显示相关值,可度量每对变量之间线性关系的程度。相关值可以介于 -1 和 +1 之间。如果两个变量倾向于同时上升和下降,则相关值为正数。如果一个变量上升而另一个变量下降,则相关值为负数。
解释
使用相关矩阵可评估两个变量之间关系的强度和方向。较高的正相关值表明这些变量度量同特征。如果这些项目并非高度相关,则可能度量不同特征或可能未明确定义。
相关
| 年龄 | 住址 | 服务处所 | 储蓄 | 外债 | |
|---|---|---|---|---|---|
| 住址 | 0.838 | ||||
| 服务处所 | 0.848 | 0.952 | |||
| 储蓄 | 0.552 | 0.570 | 0.539 | ||
| 外债 | 0.032 | 0.186 | 0.247 | -0.393 | |
| 信用卡数量 | -0.130 | 0.053 | 0.023 | -0.410 | 0.474 |
- 居住年限与年龄:0.838
- 聘用年限与年龄:0.848
- 聘用年限与居住年限:0.952
- 负债与储蓄:−0.393
- 信用卡数与年龄:−0.130
- 信用卡数与储蓄: −0.410
Spearman 相关
使用 Spearman 相关系数可以检查两个连续或顺序变量之间单调关系强度与方向。在单调关系中,变量倾向于沿着相同的相对方向移动,但不一定以恒定的速率移动。要计算 Spearman 相关,Minitab 将对原始数据进行排秩。然后,Minitab 针对已排秩数据计算相关系数。
- 强度
-
相关系数可以是介于 −1 到 +1 之间的值。系数的绝对值越大,变量之间的关系越强。
对于 Spearman 相关,绝对值 1 表明按秩排序的数据呈现完美的线性关系。例如,Spearman 相关系数 −1 表示变量 A 的最高值与变量 B 的最低值相关联,变量 A 的第二最高值与变量 B 的第二最低值相关联,以此类推。
- 方向
-
系数的符号指示关系的方向。如果两个变量都倾向于同时上升或下降,则系数为正,代表相关的直线向上倾斜。如果一个变量倾向于在另一个变量下降时上升,则系数为负,代表相关的直线向下倾斜。
下面的几幅图显示具有特定 Spearman 相关系数值的数据,以说明变量之间的关系在强度和方向上的不同模式。

无关系:Spearman rho = 0
点随机落在图上,表明变量之间无线性关系。
强正向关系:Spearman rho = .948
点靠近线,表明变量之间存在强大的关系。关系为正向,因为这两个变量同时上升。

强负向关系:Spearman rho = -1.0
点靠近线,表明变量之间存在强大的关系。关系为负向,因为当一个变量上升时,另一个变量会下降。
仅根据相关即得出一个变量会导致另一个变量更改的结论绝对不合适。只有进行过适当控制的试验才能确定是否存在因果关系。
解释
相关
| 年龄 | 住址 | 服务处所 | 储蓄 | 外债 | |
|---|---|---|---|---|---|
| 住址 | 0.824 | ||||
| 服务处所 | 0.830 | 0.912 | |||
| 储蓄 | 0.570 | 0.571 | 0.496 | ||
| 外债 | -0.198 | -0.142 | -0.056 | -0.605 | |
| 信用卡数量 | -0.179 | 0.069 | 0.036 | -0.480 | 0.353 |
配对 Spearman 相关
| 样本 1 | 样本 2 | N | 相关 | ρ 的 95% 置信区间 | P 值 |
|---|---|---|---|---|---|
| 住址 | 年龄 | 30 | 0.824 | (0.624, 0.922) | 0.000 |
| 服务处所 | 年龄 | 30 | 0.830 | (0.636, 0.926) | 0.000 |
| 储蓄 | 年龄 | 30 | 0.570 | (0.236, 0.783) | 0.001 |
| 外债 | 年龄 | 30 | -0.198 | (-0.524, 0.178) | 0.293 |
| 信用卡数量 | 年龄 | 30 | -0.179 | (-0.508, 0.197) | 0.345 |
| 服务处所 | 住址 | 30 | 0.912 | (0.798, 0.963) | 0.000 |
| 储蓄 | 住址 | 30 | 0.571 | (0.237, 0.784) | 0.001 |
| 外债 | 住址 | 30 | -0.142 | (-0.479, 0.232) | 0.454 |
| 信用卡数量 | 住址 | 30 | 0.069 | (-0.300, 0.419) | 0.719 |
| 储蓄 | 服务处所 | 30 | 0.496 | (0.144, 0.737) | 0.005 |
| 外债 | 服务处所 | 30 | -0.056 | (-0.408, 0.311) | 0.768 |
| 信用卡数量 | 服务处所 | 30 | 0.036 | (-0.328, 0.392) | 0.849 |
| 外债 | 储蓄 | 30 | -0.605 | (-0.804, -0.283) | 0.000 |
| 信用卡数量 | 储蓄 | 30 | -0.480 | (-0.726, -0.124) | 0.007 |
| 信用卡数量 | 外债 | 30 | 0.353 | (-0.020, 0.639) | 0.056 |
在这些结果中,居住年限和年龄之间的 Spearman 相关为 0.824,这表明两个变量之间存在正向关系。rho 的置信区间为 0.624 到 0.922。p 值为 0.000,这表示当显著性水平 α 为 0.05 时,关系在统计意义上显著。
负债和储蓄之间的 Spearman 相关为 -0.605,信用卡数和储蓄之间的 Spearman 相关为 -0.480。这些变量之间的关系是负向的,表明当负债和信用卡数上升时,储蓄下降。
使用的行数
使用的行数显示在“方法”表中。它是数据(包括缺失值)行的数量。
当您有缺失值时,使用的行数不等于置信区间计算中使用的实际样本数量。
相关的置信区间
置信区间提供相关系数的可能值范围。由于样本的随机性,来自总体的两个样本不可能生成相同的置信区间。但是如果将样本重复许多次,则所获得的特定百分比的置信区间或限值会包含未知的相关系数。这些包含相关系数的置信区间或限值的百分比是区间的置信水平。
例如,95% 置信水平表明,如果从总体中随机抽取 100 个样本,则大约 95 个样本将产生包含相关系数的区间。
上限定义可能大于总体差值的值。下限定义可能小于总体差值的值。
Pearson 相关的置信区间对基础二变量分布的正态性敏感。如果数据偏离正态性,那么,无论样本数量的量值是多少,置信区间都可能不准确。
Spearman 相关的置信区间基于秩,而且对基础二变量分布假设不太敏感。
解释
置信区间有助于评估结果的实际意义。使用您的专业知识可以确定置信区间是否包括对您的情况有实际意义的值。如果区间因太宽而毫无用处,请考虑增加样本数量。有关更多信息,请转到获得更加精确的置信区间的方法。
配对 Pearson 相关
| 样本 1 | 样本 2 | N | 相关 | ρ 的 95% 置信区间 | P 值 |
|---|---|---|---|---|---|
| 住址 | 年龄 | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| 服务处所 | 年龄 | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| 储蓄 | 年龄 | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| 外债 | 年龄 | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| 信用卡数量 | 年龄 | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| 服务处所 | 住址 | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| 储蓄 | 住址 | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| 外债 | 住址 | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| 信用卡数量 | 住址 | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| 储蓄 | 服务处所 | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| 外债 | 服务处所 | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| 信用卡数量 | 服务处所 | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| 外债 | 储蓄 | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| 信用卡数量 | 储蓄 | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| 信用卡数量 | 外债 | 30 | 0.474 | (0.138, 0.713) | 0.008 |
在这些结果中,居住年限和年龄之间存在正线性相关,相关值为 0.838。总体相关系数介于 0.684 和 0.920 之间的可信度为 95%。通常,相关性越强,置信区间越窄。例如,信用卡数和年龄之间的相关较弱,95% 置信区间的范围是 -0.468 到 0.242。
P 值
P 值是一个概率,用来测量否定原假设的证据。p 值越小,否定原假设的证据越充分。
解释
使用 p 值可以确定相关系数在统计意义上是否显著。
- P 值 ≤ α:相关在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出相关在统计意义上显著的结论。请使用您的专业知识确定差值在实际意义上是否显著。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:相关在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平,则决策为无法否定原假设。证据不足,无法得出相关在统计意义上显著的结论。
Pearson 相关和 Spearman 相关的 p 值程序可以很好地适应偏离正态性的情况。无论样本的父级总体如何,当 n ≥ 25 时,p 值通常准确。
配对 Pearson 相关
| 样本 1 | 样本 2 | N | 相关 | ρ 的 95% 置信区间 | P 值 |
|---|---|---|---|---|---|
| 住址 | 年龄 | 30 | 0.838 | (0.684, 0.920) | 0.000 |
| 服务处所 | 年龄 | 30 | 0.848 | (0.702, 0.926) | 0.000 |
| 储蓄 | 年龄 | 30 | 0.552 | (0.240, 0.761) | 0.002 |
| 外债 | 年龄 | 30 | 0.032 | (-0.332, 0.388) | 0.865 |
| 信用卡数量 | 年龄 | 30 | -0.130 | (-0.468, 0.242) | 0.494 |
| 服务处所 | 住址 | 30 | 0.952 | (0.901, 0.977) | 0.000 |
| 储蓄 | 住址 | 30 | 0.570 | (0.264, 0.772) | 0.001 |
| 外债 | 住址 | 30 | 0.186 | (-0.187, 0.512) | 0.326 |
| 信用卡数量 | 住址 | 30 | 0.053 | (-0.313, 0.406) | 0.779 |
| 储蓄 | 服务处所 | 30 | 0.539 | (0.222, 0.753) | 0.002 |
| 外债 | 服务处所 | 30 | 0.247 | (-0.125, 0.557) | 0.189 |
| 信用卡数量 | 服务处所 | 30 | 0.023 | (-0.340, 0.380) | 0.906 |
| 外债 | 储蓄 | 30 | -0.393 | (-0.660, -0.038) | 0.032 |
| 信用卡数量 | 储蓄 | 30 | -0.410 | (-0.671, -0.059) | 0.024 |
| 信用卡数量 | 外债 | 30 | 0.474 | (0.138, 0.713) | 0.008 |
在这些结果中,许多 p 值小于显著性水平 0.05,这表示 Pearson 相关系数在统计意义上显著。
注意
有时,由于存在极端数据点,p 值可能较小,但置信区间非常大。例如,对于信用卡数和负债,95% 置信区间非常大,但 p 值较小。当您检查矩阵图时,可能会看到极端数据点。
矩阵图
矩阵图是散点图的阵列。矩阵图中的每个散点图会在 x 和 y 轴上绘制一对项目的分值。
解释
使用该矩阵图可直观地评估每个项目或变量组合之间的关系。关系可以是线性或单调关系,也可以都不是。还可以使用矩阵图查找可能会严重影响结果的异常值。有关各种关系类型的更多信息,请转到线性、非线性和单调关系。
此矩阵图表明所有项目对都具有正线性关系。