请选择您所选的方法或公式。
置信区间 (CI)
公式
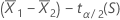 到
到 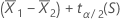
表示法
| 项 | 说明 |
|---|---|
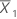 | 第一个样本的均值 |
 | 第二个样本的均值 |
| tα/2 | t 分布在 1 – α/2 处的逆累积概率 |
| α | 1 - 置信水平 / 100 |
| s | 针对检验统计量计算的样本标准差 |
T 值
公式
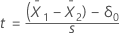
以下等式中的样本标准差 s ( ) 取决于方差假设。
) 取决于方差假设。
 ) 取决于方差假设。
) 取决于方差假设。
- 不等方差
-
在假设方差不相等时,
 的样本标准差为:
的样本标准差为:
自由度为:
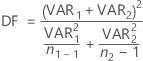
必要时,Minitab 将自由度截断为整数,此方法比圆整保守。
- 等方差
-
在假设方差相等时,公共方差由合并方差估计:
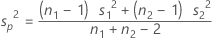
 的标准差按如下公式估计:
的标准差按如下公式估计:
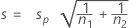
检验统计量的自由度为:
DF = n1 + n2 – 2
表示法
| 项 | 说明 |
|---|---|
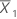 | 第一个样本的均值 |
 | 第二个样本的均值 |
| s | 以下等式的样本标准差: |
| δ0 | 两个总体均值之间的假设差值 |
| s1 | 第一个样本的样本标准差 |
| s2 | 第二个样本的样本标准差 |
| n1 | 第一个样本的样本数量 |
| n2 | 第二个样本的样本数量 |
| VAR1 | 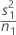 |
| VAR2 | 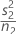 |
计算合并标准差
假设 C1 包含响应,C3 包含每个因子水平的均值。例如:
| C1 | C2 | C3 |
|---|---|---|
| 响应 | 因子 | 均值 |
| 18.95 | 1 | 14.5033 |
| 12.62 | 1 | 14.5033 |
| 11.94 | 1 | 14.5033 |
| 14.42 | 2 | 10.5567 |
| 10.06 | 2 | 10.5567 |
| 7.19 | 2 | 10.5567 |
- 选择。
- 在将结果存储在变量中中,输入 C4。
- 在表达式中,输入 SQRT((SUM((C1 - C3)**2)) / (观测值总数 - 组个数)) 。对于前面的示例,合并标准差的表达式将为:SQRT((SUM(('响应' - '均值')**2)) / (6 - 2))
Minitab 存储的值为 3.75489。
P 值
公式
P 值的计算取决于备择假设。
| 备择假设 | P 值 |
|---|---|
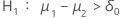 |
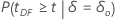 |
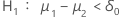 |
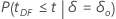 |
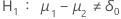 |
 |
自由度 DF 取决于方差假设。
- 不等方差
-
在假设方差不相等时,自由度为:
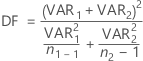
必要时,Minitab 将自由度截断为整数,此方法比圆整保守。
- 等方差
-
在假设方差相等时,检验统计量的自由度为:
DF = n1 + n2 – 2
表示法
| 项 | 说明 |
|---|---|
| μ1 | 第一个样本的总体均值 |
| μ1 | 第二个样本的总体均值 |
| n1 | 第一个样本的样本数量 |
| n2 | 第二个样本的样本数量 |
| δ0 | 两个总体均值之间的假设差值 |
| t | 样本数据的 t 统计量 |
| t | 具有 DF 自由度的 t 分布的随机变量。 |
| VAR1 | 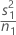 |
| VAR2 | 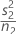 |
