关于本主题
统计量
| 项 | 说明 |
|---|---|
| 样本 i 的发生率 |
 |
| 项 | 说明 |
|---|---|
| 样本 i 中的平均发生次数 |
 |
针对正态近似的率差值的假设检验
公式
正态近似检验基于以下 Z 统计量,在下面的原假设下,该统计量的分布与标准正态分布近似:
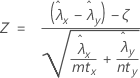
Minitab 将下面的 p 值等式用于各自的备择假设:
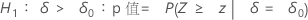
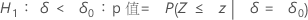

表示法
| 项 | 说明 |
|---|---|
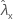 | 样本 X 的率的观测值 |
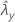 | 样本 Y 的率的观测值 |
| ζ | 两个样本的总体率之间差值的实际值 |
| ζ0 | 两个样本的总体率之间差值的假设值 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
| tx | 样本 X 的长度 |
| ty | 样本 Y 的长度 |
针对精确方法的率差值的假设检验
公式
当假设差值等于 0 时,Minitab 将使用精确过程来检验下面的原假设:
H0:ζ = λx – λy = 0,或者 H0:λx = λy
精确过程基于以下事实,假定原假设为真:
S | W ~ Binomial(w, p)
其中:


W = S + U


-
H1:ζ > 0:p 值 = P(S ≥ s | w = s + u, p = p0)
-
H1:ζ < 0:p 值 = P(S ≤ s | w = s + u, p = p0)
- H1:ζ ≠ 0:
- 如果 P(S ≤ s | w = s + u, p = p0) ≤ 0.5,或者 P(S ≥ s | w = s + u, p = p0) ≤ 0.5
则 p 值 = 2 × min {P(S ≤ s | w = s + u, p = p0),P(S ≥ s | w = s + u, p = p0)}
- 否则,p 值 = 1.0
- 如果 P(S ≤ s | w = s + u, p = p0) ≤ 0.5,或者 P(S ≥ s | w = s + u, p = p0) ≤ 0.5
其中:

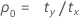
表示法
| 项 | 说明 |
|---|---|
 | 样本 X 的率的观测值 |
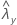 | 样本 Y 的率的观测值 |
| λx | 总体 X 的率的实际值 |
| λy | 总体 Y 的率的实际值 |
| ζ | 两个样本的总体率之间差值的实际值 |
| tx | 样本 X 的长度 |
| ty | 样本 Y 的长度 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
针对合并率方法的率差值的假设检验
使用下面的原假设检验零差值时,可以针对这两个样本使用合并率:
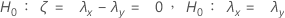
公式
合并率过程基于以下 Z 统计量,在下面的原假设下,该统计量的分布与标准正态分布近似:
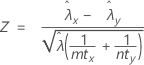
其中:
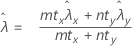
Minitab 将下面的 p 值等式用于各自的备择假设:
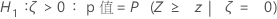
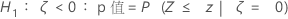
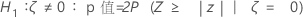
表示法
| 项 | 说明 |
|---|---|
 | 样本 X 的率的观测值 |
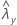 | 样本 Y 的率的观测值 |
| λx | 总体 X 的率的实际值 |
| λy | 总体 Y 的率的实际值 |
| ζ | 两个样本的总体率之间差值的实际值 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
| tx | 样本 X 的长度 |
| ty | 样本 Y 的长度 |
针对正态近似方法的均值差值的假设检验
公式
正态近似检验基于以下 Z 统计量,在下面的原假设下,该统计量的分布与标准正态分布近似。
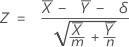
Minitab 将下面的 p 值等式用于各自的备择假设:
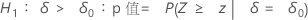
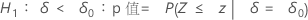

表示法
| 项 | 说明 |
|---|---|
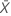 | 样本 X 中平均发生次数的观测值 |
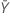 | 样本 Y 中平均发生次数的观测值 |
| δ | 两个样本的总体均值之间差值的实际值 |
| δ 0 | 两个样本的总体均值之间差值的假设值 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
针对精确方法的均值差值的假设检验
公式

精确过程基于以下事实,并假定原假设为真:
S | W ~ Binomial(w, p)
其中:


W = S + U
Minitab 将下面的 p 值等式用于各自的备择假设:
H1:δ > 0:p 值 = P(S ≥ s | w = s + u, δ = 0)
H1:δ < 0:p 值 = P(S ≤ s | w = s + u, δ = 0)
-
如果 P(S ≤ s|w = s + u, δ = 0) ≤ 0.5
或者 P(S ≥ s|w = s + u, δ = 0) ≤ 0.5
则:

- 否则,p 值 = 1.0
除非 m = n,否则双尾检验不是等尾检验。
表示法
| 项 | 说明 |
|---|---|
| μx | 总体 X 中平均发生次数的实际值 |
| μy | 总体 Y 中平均发生次数的实际值 |
| δ | 两个样本的总体均值之间差值的实际值 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
针对合并均值方法的均值差值的假设检验
公式

合并均值过程基于以下 Z 值,在下面的原假设下,该值的分布与标准正态分布近似:
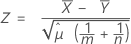
其中:
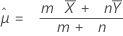
Minitab 将下面的 p 值等式用于各自的备择假设:



表示法
| 项 | 说明 |
|---|---|
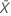 | 样本 X 中平均发生次数的观测值 |
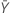 | 样本 Y 中平均发生次数的观测值 |
| µx | 总体 X 中平均发生次数的实际值 |
| µy | 总体 Y 中平均发生次数的实际值 |
| δ | 两个样本的总体均值之间差值的实际值 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
率差值的置信区间
公式
两个总体 Poisson 率之间差值的 100(1 – α)% 置信区间的计算公式如下:
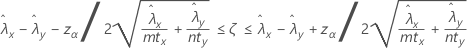
表示法
| 项 | 说明 |
|---|---|
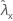 | 样本 X 的率的观测值 |
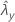 | 样本 Y 的率的观测值 |
| ζ | 两个样本的总体率之间差值的实际值 |
| zx | 标准正态分布的 x 百分位点上限,其中 0 < x < 1 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
| tx | 样本 X 的长度 |
| ty | 样本 Y 的长度 |
率差值的置信界限
公式
在指定“大于”检验时,两个总体 Poisson 率之间差值的 100(1 – α)% 置信下限的计算公式如下:
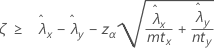
当您指定“小于”检验时,两个总体 Poisson 率之间差值的 100(1 – α)% 置信上限的计算公式如下:
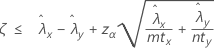
表示法
| 项 | 说明 |
|---|---|
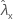 | 样本 X 的率的观测值 |
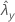 | 样本 Y 的率的观测值 |
| ζ | 两个样本的总体率之间差值的实际值 |
| zx | 标准正态分布的 x 百分位点上限,其中 0 < x < 1 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
| tx | 样本 X 的长度 |
| ty | 样本 Y 的长度 |
均值差值的置信区间
公式
两个总体 Poisson 均值之间差值的 100(1 – α)% 置信区间的计算公式如下:
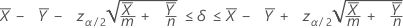
表示法
| 项 | 说明 |
|---|---|
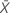 | 样本 X 中平均发生次数的观测值 |
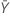 | 样本 Y 中平均发生次数的观测值 |
| δ | 两个样本的总体均值之间差值的实际值 |
| zx | 标准正态分布的 x 百分位点上限,其中 0 < x < 1 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
均值差值的置信界限
公式
在指定“大于”检验时,两个总体 Poisson 均值之间差值的 100(1 – α)% 置信下限的计算公式如下:
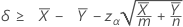
在指定“小于”检验时,两个总体 Poisson 均值之间差值的 100(1 – α)% 置信上限的计算公式如下:
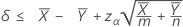
表示法
| 项 | 说明 |
|---|---|
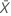 | 样本 X 中平均发生次数的观测值 |
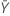 | 样本 Y 中平均发生次数的观测值 |
| δ | 两个样本的总体均值之间差值的实际值 |
| zx | 标准正态分布的 x 百分位点上限,其中 0 < x < 1 |
| m | 样本 X 的样本数量 |
| n | 样本 Y 的样本数量 |
