请选择您所选的方法或公式。
置信区间 (CI)
公式
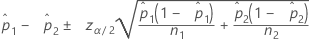
表示法
| 项 | 说明 |
|---|---|
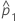 | 第一个总体比率的估计值 |
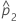 | 第二个总体比率的估计值 |
| n1 | 第一个样本中的试验数 |
| n2 | 第二个样本中的试验数 |
| zα/2 | 标准正态分布在 1 – α/2 处的逆累积概率 |
| α | 1 – 置信水平/100 |
正态近似检验
检验统计量 Z 的计算取决于用来估计 p 的方法。
- p 的不同估计值
- 默认情况下,Minitab 对每个总体使用不同的 p 估计值并按如下方式计算 Z:
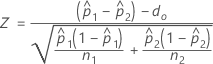
- p 的合并估计值
- 如果假设检验差值是零,您选择针对检验使用 p 的合并估计值,Minitab 将按如下方式计算 Z:
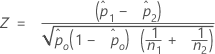
每个备择假设的 p 值为:
- H1:p1 > p2:p 值 = P(Z1 ≥ z)
- H1:p1 < p2:p 值 = P(Z1 ≤ z)
- H1:p1 ≠ p2:p 值 = 2P(Z1 ≥ z)
计算这些标准正态分布的概率。
表示法
| 项 | 说明 |
|---|---|
| p1 | 第一个总体中的事件所占的实际比率 |
| p2 | 第二个总体中的事件所占的实际比率 |
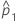 | 第一个样本中观测到事件的比率 |
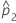 | 第二个样本中观测到事件的比率 |
| n1 | 第一个样本中的试验数 |
| n2 | 第二个样本中的试验数 |
| d0 | 第一个总体与第二个总体之间的假设差值 |
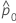 | 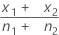 |
| x1 | 第一个样本中的事件数 |
| x2 | 第二个样本中的事件数 |
Fisher 精确检验
Minitab 除了执行基于正态近似的检验外,还执行 Fisher 精确检验。Fisher 精确检验对于所有的样本数量均有效。
公式
在原假设下,第一个样本 (x1) 中的事件数服从具有如下参数的超几何分布:
- 总体大小 = n1 + n2
- 总体中的事件数 = x1 + x2
- 样本数量 = n1
假设 f( ) 和 F( ) 分别表示这个超几何分布的 PDF 和 CDF。假设众数表示分布众数。每个备择假设的 p 值如下所示:
- H1:p1 < p2
p 值 = F(x1)
- H1:p1 > p2
p 值 = 1 – F(x1 – 1)
- H1:p1 ≠ p2
存在三种情况:
- 第 1 种情况:x1 < 众数
p 值 = p 值下限 + p 值上限
项 说明 p 值下限 F(x1) p 值上限 1 – F(y – 1) y 最小整数 > 众数,因此 f(y) <f(x1) 注意
p 值上限可能等于零。
- 第 2 种情况:x1 = 众数
p 值 = 1.0
- 第 3 种情况:x1 > 众数
p 值 = p 值下限 + p 值上限
项 说明 p 值上限 1 – F(x1 – 1) p 值下限 F(y) y 最大整数 < 众数,因此 f(y) < f(x1) 注意
p 值下限可能等于零。
- 第 1 种情况:x1 < 众数
表示法
| 项 | 说明 |
|---|---|
| p1 | 第一个总体中的事件所占的实际比率 |
| p2 | 第二个总体中的事件所占的实际比率 |
| x1 | 第一个样本中的事件数 |
| x2 | 第二个样本中的事件数 |
| n1 | 第一个样本中的试验数 |
| n2 | 第二个样本中的试验数 |
