步骤 1:确定总体均值的置信区间
首先考虑样本均值,然后检查置信区间。
样本数据的均值是对总体均值的估计值。由于均值基于样本数据而不是整个总体,因此样本均值通常不等于总体均值。使用置信区间可以更好地估计总体均值。
置信区间提供总体均值的可能值范围。例如,95% 置信水平表明,如果从总体中随机抽取 100 个样本,则大约 95 个样本将产生包含总体均值的区间。置信区间有助于评估结果的实际意义。使用您的专业知识可以确定置信区间是否包括对您的情形有实际意义的值。如果区间因太宽而毫无用处,请考虑增加样本数量。有关更多信息,请转到获得更加精确的置信区间的方法。
描述性统计量
| N | 均值 | 标准差 | 均值标准误 | μ 的 95% 置信区间 |
|---|---|---|---|---|
| 20 | 16.460 | 2.258 | 0.581 | (15.321, 17.599) |
主要结果:均值、95% 置信区间
在这些结果中,脂肪百分比的总体均值估计值为16.46%。总体均值介于 15.321% 和 17.599% 之间的可信度为 95%。
步骤 2:确定检验结果在统计意义上是否显著
- P 值 ≤ α:均值的差值在统计意义上显著(否定 H0)
- 如果 p 值小于或等于显著性水平,则决策为否定原假设。您可以得出总体均值和假设均值的差值在统计意义上显著的结论。请使用您的专业知识确定差值在实际意义上是否显著。有关更多信息,请转到统计显著性和实际显著性。
- P 值 > α:均值的差值在统计意义上不显著(无法否定 H0)
- 如果 p 值大于显著性水平,则决策为无法否定原假设。您没有足够的证据得出总体均值与假设均值的差值在统计意义上显著的结论。您应该确保检验具有足够的功效来检测到在实际意义上显著的差值。有关更多信息,请转到单样本 Z 的功效和样本数量。
描述性统计量
| N | 均值 | 标准差 | 均值标准误 | μ 的 95% 置信区间 |
|---|---|---|---|---|
| 20 | 16.460 | 2.258 | 0.581 | (15.321, 17.599) |
检验
| 原假设 | H₀: μ = 15 |
|---|---|
| 备择假设 | H₁: μ ≠ 15 |
| Z 值 | P 值 |
|---|---|
| 2.51 | 0.012 |
主要结果:P 值
在这些结果中,原假设声明平均脂肪百分比为 15%。由于 p 值为 0.012(小于显著性水平 0.05),因此决策为否定原假设并得出总体平均脂肪百分比不同于 15% 的结论。
步骤 3:检查数据是否有问题
您数据中存在的问题(如偏度和异常值)可对结果产生不利影响。可使用图形来查找偏度以及确定可能的异常值。
检查数据的散布以确定数据看上去是否偏斜。
当数据偏斜时,大多数数据位于图形的高或低侧。通常情况下,在直方图或箱线图中最易于检测偏度。
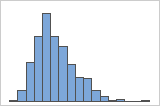
右偏斜
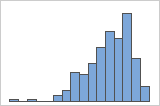
左偏斜
带右偏斜数据的直方图显示等待时间。大部分等待时间相对较短,只有少数等待时间很长。带左偏斜数据的直方图显示失效时间数据。少数几个项立即失败,更多的项会在随后失败。
如果您的样本小(小于 20 个值),严重偏斜的数据可影响 p 值的有效性。如果您的数据严重偏斜,并且样本较小,请考虑增大样本数量。
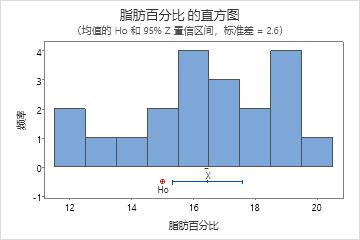
在该直方图中,数据的偏斜程度似乎不严重。
识别异常值
异常值是远离其他数据值的数据值,可以显著影响您的分析结果。通常情况下,在箱线图上最容易识别异常值。
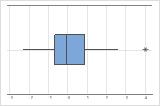
在箱线图上,星号 (*) 表示异常值。
尝试确定导致任何异常值的原因。更正任何数据输入错误或测量误差。考虑删除异常、单次事件(也称为特殊原因)的数据值。然后,重新执行分析。有关更多信息,请转到标识异常值。
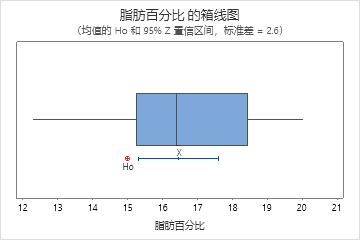
在该箱线图中,没有异常值。
