统计量
| 项 | 说明 |
|---|---|
| 发生率 |
 |
| 平均发生次数 |
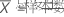 |
发生率等于每单位的观测值长度的平均发生次数。均值是整个样本中的平均发生次数。如果长度等于 1,则发生率等于均值。
精确检验的 p 值
公式
- H1:λ > λ0:p 值 = P(S ≥ s | λ = λ0),其中 S 服从均值为 nλ0t 的 Poisson 分布。
- H1:λ < λ0:p 值 = P(S ≤ s | λ = λ0),其中 S 服从均值为 nλ0t 的 Poisson 分布。
- H1:λ ≠ λ0:Minitab 使用似然比检验,如下所示:
定义函数 G(s),该函数用 s(Poisson 过程中的总发生次数)表示似然比检验:

- 如果 0 ≤ s < nλ0t,则通过等式 G(y) = G(s) 对区间 (nλ0t, enλ0t] 中的 y 求解;
p 值 = P(S ≤ s | λ = λ0) + P(S ≥ y | λ = λ0)
- 如果 s = nλ0t,则
p 值 = 1.00
- 如果 nλ0t < s ≤ enλ0t,则通过等式 G(y) = G(s) 对区间 [0, nλ0t) 中的 y 求解;
p 值 = P(S ≤ y | λ = λ0) + P(S ≥ s | λ = λ0)
- 如果 s > enλ0t,则检验是单侧的,且
p 值 = P(S ≥ s | λ = λ0)
其中,S 服从均值为 nλ0t 的 Poisson 分布。
- 如果 0 ≤ s < nλ0t,则通过等式 G(y) = G(s) 对区间 (nλ0t, enλ0t] 中的 y 求解;
表示法
| 项 | 说明 |
|---|---|
| s | Poisson 过程中的总发生次数 |
| t | 观测值的“长度” |
| λ0 | 总体率参数的假设值 |
| λ | 总体率参数的实际值 |
| n | 样本数量 |
| e | 大约 2.71828 |
精确检验的置信区间和置信界限
置信区间
Poisson 过程发生率的精确 100(1 – α)% 置信区间的计算公式如下:
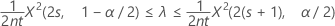
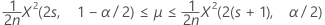
置信界限
如果您指定单侧检验,Minitab 会根据备择假设的方向计算单侧 100(1 – α)% 置信界限。
-
如果您指定“大于”备择假设,则率的精确 100(1 – α)% 下限的计算公式如下:
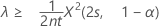
均值的精确 100(1 – α)% 下限的计算公式如下:
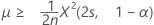
-
如果您指定“小于”备择假设,则率的精确 100(1 – α)% 上限的计算公式如下:
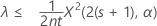
均值的精确 100(1 – α)% 上限的计算公式如下:
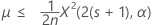
表示法
| 项 | 说明 |
|---|---|
| s | Poisson 过程中的总发生次数 |
| t | 观测值的“长度” |
| λ | 总体率的实际值 |
| μ | 总体均值的实际值 |
| Χ2(p, x) | 自由度为 P 的 Χ2 分布的 x 百分位点上限,其中 0 < x < 1。 |
| α | 100(1–α)% 置信区间的 alpha 水平 |
| n | 样本数量 |
正态近似的 p 值
当总发生次数大于 10 时,正态近似有效。
公式
基于 单样本 Poisson 率 的正态近似的假设检验将下面的 p 值等式用于各自的备择假设:


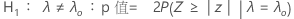
表示法
| 项 | 说明 |
|---|---|
| Z | 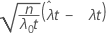 |
| t | 观测值的“长度” |
| λ 0 | 总体率参数的假设值 |
| λ | 总体率参数的实际值 |
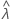 | 样本率统计量的观测值 |
| n | 样本数量 |
正态近似的置信区间和置信界限
置信区间
Poisson 过程发生率的 100(1 – α)% 置信区间基于正态近似,按如下公式计算:
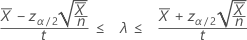
在指定“长度”的值时,Minitab 还显示平均发生次数的置信区间。该置信区间的计算公式如下:
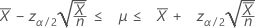
置信界限
如果您指定单侧检验,Minitab 会根据备择假设的方向计算单侧 100(1 – α)% 置信界限。-
如果您指定“大于”备择假设,则率的精确 100(1 – α)% 下限的计算公式如下:
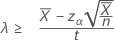
如果您指定“长度”的值,则均值的精确 100(1-α)% 下限的计算公式如下:
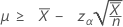
-
如果您指定“小于”备择假设,则率的精确 100(1 – α)% 上限的计算公式如下:
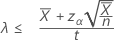
如果您指定“长度”的值,则均值的精确 100(1 – α)% 上限的计算公式如下:
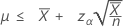
表示法
| 项 | 说明 |
|---|---|
| s | Poisson 过程中的总发生次数 |
| t | 观测值的“长度” |
| λ | 总体率的实际值 |
| μ | 总体均值的实际值 |
| Zx | 标准正态分布的 x 百分位点上限,其中 0 < x < 1。 |
| α | 100(1–α)% 置信区间的 alpha 水平 |
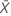 | 样本中的平均发生次数 |
| n | 样本数量 |
