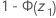关于本主题
调整后的 Blaker 精确置信区间和测试方法
调整后的 Blaker 精确方法为事件比例生成双侧置信区间,并为 p ≠ p0的备择假设生成 p值。 Blaker12 通过反转精确检验的 p 值函数来提供精确的双侧置信区间。Clopper-Pearson 区间较宽,并且始终包含 Blaker 置信区间。将 Blaker 精确方法中的间隔嵌套在一起。此属性意味着具有较高置信度的置信区间包含具有较低置信度的置信区间。例如,精确的双侧 Blaker 95% 置信区间包含相应的 90% 置信区间。
Blaker 的原始精确方法有两个局限性。一个局限性是计算置信区间的数值算法很慢,尤其是在样本量很大的情况下。另一个限制是,对于某些数据,当 p 值小于与置信水平相对应的显著性水平时,原始 Blaker 精确方法会生成一个涵盖假设比例的区间。当 p 值大于对应于置信水平的显著性水平时,当置信区间不包含假设比例时,也会出现限制。
为了克服这些限制,Minitab Statistical Software 中的分析使用 Klaschka 和 Reiczigel 的算法生成置信区间和 p 值。3此方法的名称是调整后的 Blaker 精确方法。这种数值算法的计算速度更快,并生成总体上一致的置信区间和检验。调整后的 Blaker 置信区间也是精确且嵌套的。
对于小于或大于的备择假设,分析使用 Clopper-Pearson 精确方法。
Clopper-Pearson 精确置信区间法
区间 (PL, PU) 是 p的双侧 100(1 – α)% 置信区间。当样本没有事件时,下限为 0。当样本仅包含事件时,上限为 1。
下限
公式
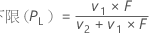
表示法
| 项 | 说明 |
|---|---|
| v1节 | 2x |
| v2节 | 2(n – x + 1) |
| x | 事件数 |
| n | 试验数 |
| F | 自由度为 v1 和 v2 的 F 分布的 α/2 下限点 |
上限
公式
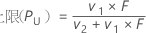
表示法
| 项 | 说明 |
|---|---|
| 第1节 | 2(x + 1) |
| v2节 | 2(n – x) |
| x | 事件数 |
| n | 试验数 |
| F | 自由度为 v1 和 v2 的 F 分布的 α/2 上限点 |
对应于 Clopper-Pearson 精确置信区间的检验
公式
- Ha:第 ≠ 页0
- p 值 =
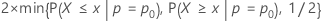
- Ha: p > p0
- p 值 = P{ X ≥ x | p = po}
- Ha:p < p0
- p 值 = P{ X ≤ x | p = po}
表示法
| 项 | 说明 |
|---|---|
| p0 | 假设比率 |
| n | 试验数 |
| p | 事件的概率 |
| x | 事件数 |
威尔逊评分置信区间法
威尔逊4 反转分数检验以获得 Minitab Statistical Software 命名为 Wilson 分数置信区间的置信区间。威尔逊评分区间有两种形式,一种没有连续性校正,另一种有连续性校正。没有校正的区间覆盖率有时低于标称置信水平。校正区间的实际置信水平至少为名义置信水平。对于这两种方法,当样本没有事件时,则下限为 0。当样本仅包含事件时,上限为 1。
没有连续性校正的间隔
双侧 100(1 – α)% 置信区间的公式如下:
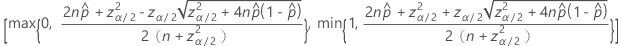
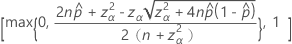
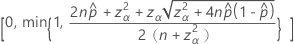
连续性校正的间隔
双侧 100(1 – α)% 区间的下限公式如下:
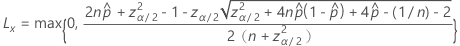
双侧 100(1 – α)% 区间的上限公式如下:
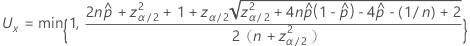
单侧 100(1 – α)% 下限的公式如下:
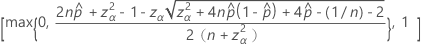
单侧 100(1 – α)% 上限的公式如下:
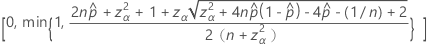
表示法
| 项 | 说明 |
|---|---|
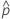 | 观测概率, 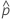 = x / n = x / n |
| x | 事件数 |
| n | 试验数 |
| zγ | 标准正态分布的上百分位数点, γ |
| α | 1 – 置信水平/100 |
分数测试
没有连续性校正的方法
对应于 Wilson 分数置信区间和正态近似方法(Web 应用)的检验是众所周知的分数检验。分数检验统计量的公式如下:
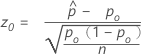
- Ha:p ≠ p0
- p 值 =
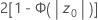
- Ha:p > p0
- p 值 =

- Ha:p < p0
- p 值 =

具有连续性校正的方法
具有连续性校正的过程的检验统计量和 p 值取决于备择假设。
- Ha:p ≠ p0
-

- Ha:p > p0
-
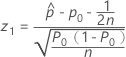
- Ha:p < p0
-
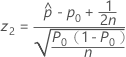
表示法
| 项 | 说明 |
|---|---|
 | 观测到的概率 x/n |
| x | 事件数 |
| n | 试验数 |
| p0 | 假设比率 |
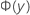 | y处标准正态分布的累积分布函数 |
Agresti-Coull 置信区间和测试方法
置信区间
Agresti 和 Coull5 对置信区间的 Wald 方法进行了调整,从而改善了覆盖率属性。对于双侧 95% 置信区间,调整大约将 2 个事件和 2 个非事件相加,然后根据 Wald 置信区间公式的公式计算置信区间。当样本没有事件时,下限为 0。当样本仅包含事件时,上限为 1。
双侧 100(1 – α)% 区间的公式如下:
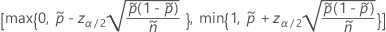
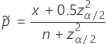
和
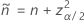
单侧 100(1 – α)% 下限的公式如下:
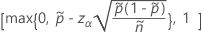
单侧 100(1 – α)% 上限的公式如下:
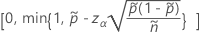
对于单侧限制,请使用  在定义中
在定义中 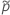 和
和 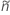 :
:
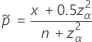
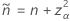
对应于 Agresti-Coull 区间的检验
该分析通过反转置信区间过程来计算检验的 p 值。
表示法
| 项 | 说明 |
|---|---|
| x | 事件数 |
| n | 试验数 |
| zγ | 标准正态分布的上百分位数点, γ |
| α | 1 – 置信水平/100 |
Wald 正态近似的置信区间(Web 应用程序)
公式
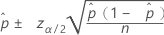
表示法
| 项 | 说明 |
|---|---|
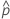 | 观测概率, 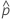 = x / n = x / n |
| x | n 个试验中观测到的事件数 |
| n | 试验数 |
| Zα/2 | 标准正态分布在 1–α/2 处的逆累积概率 |
| α | 1 – 置信水平/100 |